今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第1話 サイン波のかけ算
ご挨拶
「Mr.Smithとインピーダンスマッチングの話」を愛読いただきまして有り難うございました。おかげさまでFB NEWS編集部から、新しいテーマで新連載を書くようご依頼を頂きました。
本誌はアマチュア無線家向けのWEBマガジンですが、「Mr.Smithとインピーダンスマッチングの話」と同様、プロやセミプロ向けの技術連載も取りそろえたいとのことですので、無線通信機の設計に携わるプロやセミプロのエンジニアを対象に、無線工学や電子工学の
・ 「そんなの常識」と思っていたけれど、いざ人から聞かれると説明できない事
・ 「そんなの判っているよ」と思っていたけれど、目から鱗の話
・ 「大学で学んだけど、よく解らなくて」でも今まで何とかなってきた事
といった、「今更人には聞けない話」を切り口に、無線通信の基礎について解説する連載を書かせて頂こうと思います。これまでと同様、計算式のみの解説を極力避けて、多少乱暴でも具体的イメージを持って理解していただく事を執筆方針とします。「厳密には間違い」という部分については大目に見て頂けますと幸いです。
第1話 サイン波のかけ算
「今更人にはきけない話」の最初のテーマは「かけ算」です。無線機の中にはかけ算処理や、アナログのかけ算回路が多用されています。そしてアナログ信号のかけ算処理を担うのが「ミキサ回路」なのですが、増幅回路やフィルタなどと違い、ミキサ回路の動作は教科書での解説も少なく、理解できているようで理解できていない方が多いのではないかと思います。新連載の最初はこの「サイン波のかけ算とかけ算回路」をテーマとして取り上げさせて頂きます。
1. サイン波のかけ算とその使い道
まず言葉の定義をしておきます。
「サイン波のかけ算」というと、2種類の演算が考えられます。
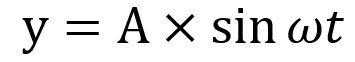
→ サイン波をA倍する ・・・ (式1-1)
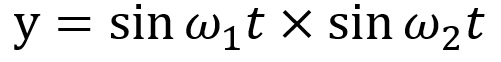
→ サイン波とサイン波のかけ算 ・・・ (式1-2)
本連載で「サイン波のかけ算」と表記した時は、特に断りがない限り、(式1-2)に示した「サイン波とサイン波のかけ算」を示します。ちなみに(式1-1)は「サイン波の増幅」です。
細かい話を始める前に、無線通信機の信号処理の中でどれくらい「かけ算」をしているか、表1-1に整理してみました。
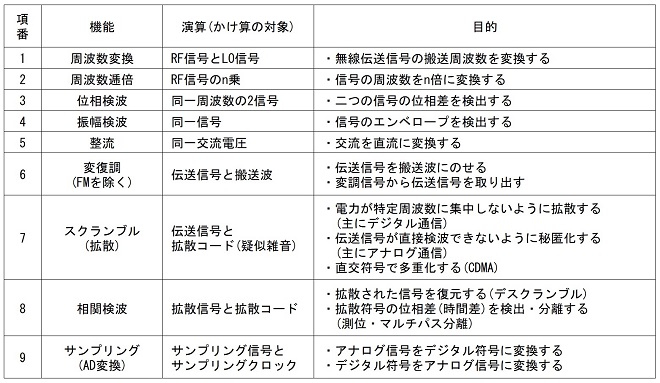
表1-1 無線通信機で使われるかけ算
このうち項番9はサンプリング(離散値化)処理が「かけ算」であって、AD変換がかけ算と言うわけではありません。
如何ですか? 図1に示した一般的な無線通信機の送受信部の構成図を見ると、増幅、発振とフィルタリングを除けば、残りはほぼ全部「かけ算」であることがおわかり頂けると思います。
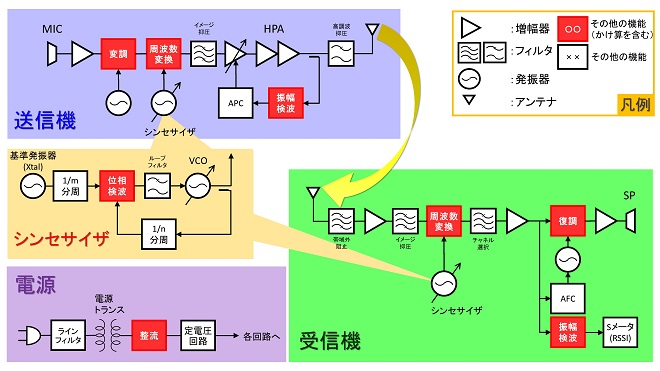
図1 一般的な無線通信機の構成(アナログ単信方式・多重なし)
これほどあちこちで使いまくっている「かけ算」なのに増幅、発振、フィルタと比べて「かけ算」を取り扱う文献はとても少ないと思いませんか。「そんなの一演算に過ぎないのだから当たり前だろ」と言われそうですね。でも、アナログ回路で処理するかけ算は意外に奥が深かったりしますので、ちょっと捻くれた目線で無線機の要素技術を分析するのも楽しいのではないかと思います。
2. なぜそんなにかけ算するのか?
なぜそんなにかけ算が多用されるのでしょうか。それは無線通信に利用される信号操作の殆どが、信号周波数の変換と復元、もしくは交流から直流への変換だからです。ベースになるのは、高校の数ⅡBで学んだ「三角関数の加法定理」です。 → (式2-1)~(式2-4)
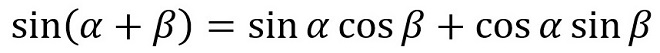
(式2-1)
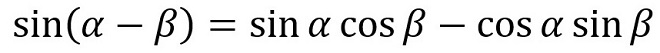
(式2-2)
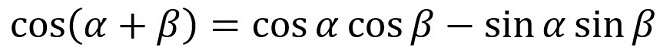
(式2-3)
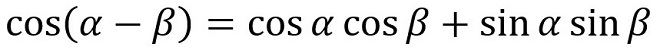
(式2-4)
“tan”の加法定理もありますが、ここでは省略します。我々電気屋(特に無線屋)が多用する「かけ算」は、これらの式を変形した (式2-5)~(式2-8)です。
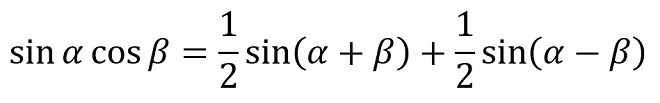
(式2-5)
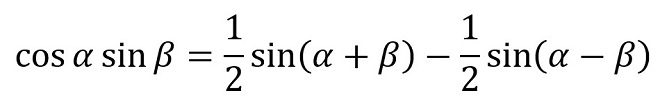
(式2-6)
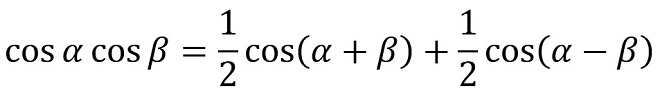
(式2-7)
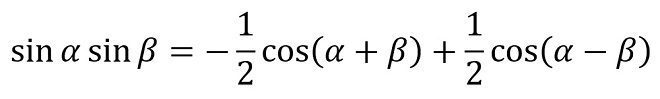
(式2-8)
筆者も含め皆さん高校生の頃は細かいことは考えずに丸暗記したのではないでしょうか。レベルの高い大学を受験された方は定理の証明までクリアされていると思います。数ⅡBで登場する三角関数はあくまで三角形の世界であって三角関数の引数α、β は「角度」でしたが、我々電気屋は引数α、β にω1t、ω2t (厳密には位相を考慮する必要があるので ω1t +φ1、ω2t +φ2 )を代入します。
つまり「サイン波」のかけ算です。ここでωは「角速度[rad/sec]」というパラメータで、一秒あたり何radian角度が進む(=回転する)かを示す値です。我々電気屋はこれをサイン波の周波数を示すパラメータと捉え、ω=2π𝑓 (𝑓は周波数[Hz]=[cycles/sec])という値を代入し、角周波数と呼ぶ...は無線従事者免許をお持ちの方なら常識のレベルかと思います。
実際に(式2-7)にω1t、ω2t を代入してみましょう(位相φ は省略します)。
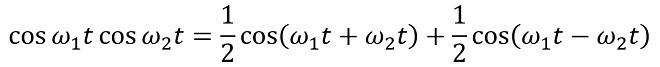
(式2-9)
ω=2π𝑓ですから
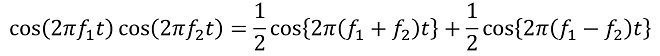
(式2-10)
つまり(式2-10)は図2に示すように、振幅の等しい周波数𝑓1のサイン波と周波数𝑓2のサイン波をかけ算すると、振幅が半分で、周波数が𝑓1+𝑓2ならびに𝑓1-𝑓2の2つのサイン波に変換されると言うことを示しています。
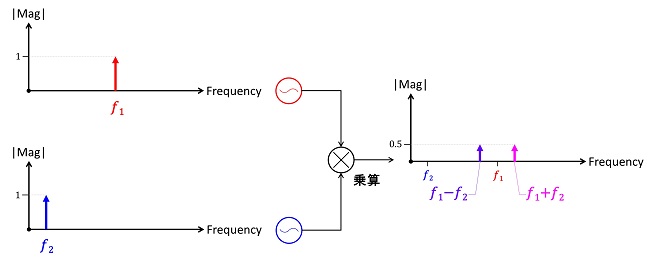
図2 振幅が等しく周波数の異なるサイン波をかけ算したときの周波数領域でのレスポンス
(式2-7)を用いて解説しましたが、他の式でも位相関係が変化するだけで、周波数スペクトルの絶対値で見れば、結果は同じになります。これは周波数変換の基本原理で、無線従事者国家試験を受験された方なら皆さん学ばれた事と思います。
3. それってどんな波形なの?
無線工学の教科書に登場する解説は概ね図2までで、私も含め、皆さん周波数変換という操作を理解したつもりになるのですが、実際にサイン波どうしを時間領域でかけ算するとどのような波形になるから図2の結果に至るのでしょうか。実際のかけ算回路の動作を理解するためには、サイン波をかけ算したときの時間領域での波形を理解することが重要です(と私は思っています)。
私が学生の頃は頭の中で考えるか、FORTRANかBASICでプログラムを作成してPC画面に書かせてみるか、はたまた実際のミキサの波形をオシロスコープで眺めるか、というような方法しがなかったのですが、今は表計算アプリで簡単に計算することができます。
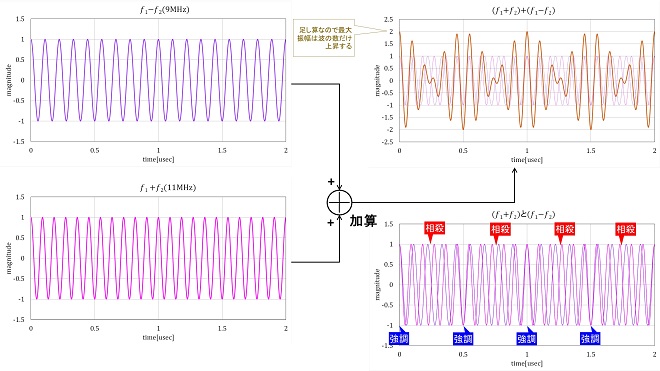
ここでは10MHzの信号に、振幅の等しい1MHzの正弦波(COS波)をかけ算してみることにします。結果を図3に示します。
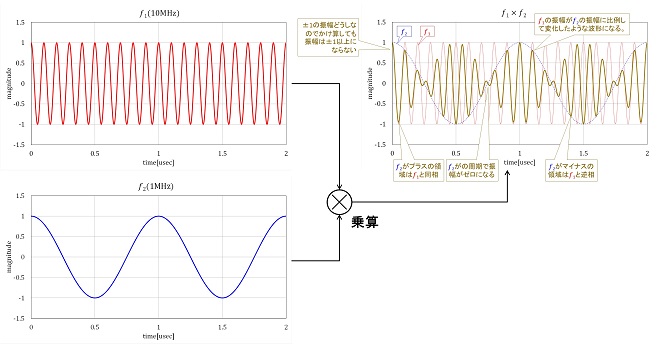
図3 振幅が等しく周波数の異なるサイン波をかけ算したときの時間領域でのレスポンス
正弦波は振幅が±1なので、これをいくつ掛け合わせても最大振幅は1です。図3に示した通り、両者の波形のかけ算なので10MHzの正弦波が0.5µsec(1MHzの半周期)ごとに振幅ゼロ→位相反転を繰り返し、振幅に1MHzのエンベロープが現れる波形になります。
さて、この波形は本当に𝑓1−𝑓2(=9MHz)と𝑓1+𝑓2(=11MHz)の和なのでしょうか。今度は9MHzと11MHzを足し算してみた結果を図4に示します。
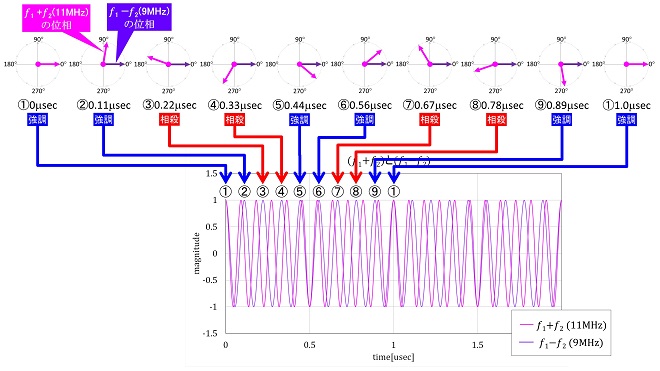
正弦波は周期関数なので、周波数の異なる2波を足し算すると、周期的に同位相になるタイミングと逆位相になるタイミングが発生します。この様子を図5に示します。
ここでは9MHzと11MHzの正弦波を合成した結果を示していますので、両者が同相からスタートしたとすると、9MHzの位相ベクトルが1サイクル回転する間に11MHzの位相ベクトルは11/9サイクル(1.22サイクル)回転します。つまり2/9サイクル早く電圧が遷移します。この結果、両者が同じ振幅の場合、振幅が2倍になるタイミングとゼロになるタイミングは、それぞれ9MHzの信号で観測して9/2 = 4.5サイクル(=0.5µsec)毎に発生し、振振幅最大点と相殺点の間隔は、その半分の9/4=2.25サイクル(=0.25µsec)となります。結果、図4の加算結果に示すように両者の差周波数の周期で振幅の強弱が発生・・・ 所謂「ビート(うなり)」が発生します。図3の結果は「うなり」波形がかけ算でも生成できることを示しており、図4の加算結果を図3の乗算結果と比較してみると、図4の加算結果の振幅が2倍になっている以外、同じ波形になっていることがお判り頂けますね。10MHzと1MHzの積は9MHzと11MHzの和に等しい。これが三角関数の加法定理が示す本質的なところといえます。
4. 第1話のまとめ
以下、第1話の要点を整理します。
① 無線通信機器に適用される主要な回路技術は増幅、発振、フィルタリング、そしてサイン波のかけ算である。
② 周波数の異なる2つのサイン波をかけ算すると三角関数の加法定理に従い、両者の和の周波数と差の周波数が生成される。
今回お話した内容は、大半が高校の数学Ⅱ、物理Ⅰの復習のような内容でした。解説を割愛しましたが、(式2-5)、(式2-6)、(式2-8)を用いて考えても結果は同じになります。これらの計算式は2つのサイン波の位相差の違いを示しています。解説に使用したグラフはMicrosoft🄬Excel🄬※1で作成しましたが、ここからダウンロード※2できるようにして頂きますので、興味のある方は位相を変化させたりして遊んでみるとイメージがわきやすいと思います。
実際に2つの信号をかけ算する為には、ディジタル信号処理を行うか、かけ算回路を使用する事になるのですが、高周波信号をかけ算したり、電力効率を考える必要があったりする場合、かけ算に使用する回路に色々と工夫が必要です。次回以降、今回お話した「サイン波のかけ算」が無線機の回路用途毎にどのように実装されているのか解説していきたいと思います。
※1: Microsoft、ならびにExcelはマイクロソフト社の商標です。
※2: ダウンロードされたExcelシートに関するご質問についてはご容赦ください。これらExcelシートの内容に関する知的財産権その他一切の権利は筆者である濱田倫一に帰属します。月刊FB NEWS編集部は筆者 濱田倫一の許可を得て本件記事を掲載しております。また筆者、ならびに月刊FB NEWS編集部は、これらExcelシートの二次使用に伴う一切の責任を負いませんので、あらかじめご了承ください。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
お知らせ
-
2022.11.15
11月号後半の記事をアップしました
-
2022.11.1
11月号の記事をアップしました
-
2022.10.17
10月号後半の記事をアップしました
-
2022.10.3
10月号の記事をアップしました
-
2022.9.15
9月号後半の記事をアップしました
-
2022.9.1
9月号の記事をアップしました
-
2022.8.15
8月号後半の記事をアップしました
-
2022.8.1
8月号の記事をアップしました
-
2022.7.15
7月号後半の記事をアップしました
-
2022.7.1
7月号の記事をアップしました
-
2022.6.15
6月号後半の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JL3ZGL」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2022.6.1
6月号の記事をアップしました
6月4日(土)、JH1CBX/3が14MHz SSBに初オンエアします。 入感がありましたらぜひお声がけください。 -
2022.5.16
5月号後半の記事をアップしました
-
2022.5.2
5月号の記事をアップしました
5月14日(土)、JL3ZGLはオペレーターにMasacoさんを迎えHAMtte交信パーティに 参加します。詳しくは4月号のニュースをご確認ください。 -
2022.4.15
4月号後半の記事をアップしました
-
2022.4.1
4月号の記事をアップしました
-
2022.3.15
3月号後半の記事をアップしました
-
2022.3.1
3月号の記事をアップしました
-
2022.2.15
2月号後半の記事をアップしました
-
2022.2.1
2月号の記事をアップしました
-
2022.1.17
1月号後半の記事をアップしました
-
2022.1.5
1月号の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JA3YUA」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2021.12.15
12月号後半の記事をアップしました
-
2021.12.1
12月号の記事をアップしました
-
2021.11.15
11月号後半の記事をアップしました
-
2021.11.01
2021年11月号の記事をアップしました
-
2021.10.15
10月号後半の記事をアップしました
-
2021.10.01
2021年10月号の記事をアップしました
-
2021.09.15
9月号後半の記事をアップしました
-
2021.09.01
2021年9月号の記事をアップしました
-
2021.08.16
8月号後半の記事をアップしました
-
2021.08.02
2021年8月号の記事をアップしました
-
2021.07.15
7月号後半の記事をアップしました
-
2021.07.01
2021年7月号の記事をアップしました
-
2021.06.15
6月号後半の記事をアップしました
-
2021.06.01
2021年6月号の記事をアップしました
-
2021.05.17
5月号後半の記事をアップしました
-
2021.05.06
2021年5月号の記事をアップしました
-
2021.04.15
4月号後半の記事をアップしました
-
2021.04.01
2021年4月号の記事をアップしました
連載記事 Masacoの「むせんのせかい」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.15
3月号後半の記事をアップしました
連載記事「今月のハム」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.01
2021年3月号の記事をアップしました
-
2021.02.15
2月号後半の記事をアップしました
-
2021.02.01
2021年2月号の記事をアップしました
-
2021.01.15
1月号後半の記事をアップしました
-
2021.01.05
2021年1月号の記事をアップしました
-
2020.12.15
12月号後半の記事をアップしました
-
2020.12.01
2020年12月号の記事をアップしました
-
2020.11.16
11月号後半の記事をアップしました
-
2020.11.02
2020年11月号の記事をアップしました
-
2020.10.15
10月号後半の記事をアップしました
-
2020.10.01
2020年10月号の記事をアップしました
-
2020.09.15
9月号後半の記事をアップしました
-
2020.09.01
2020年9月号の記事をアップしました
-
2020.08.17
8月号後半の記事をアップしました
-
2020.08.03
2020年8月号の記事をアップしました
-
2020.07.15
7月号後半の記事をアップしました
-
2020.07.01
2020年7月号の記事をアップしました
-
2020.06.15
6月号後半の記事をアップしました
-
2020.06.01
2020年6月号の記事をアップしました
-
2020.05.01
2020年5月号の記事をアップしました
-
2020.04.15
4月号後半の記事をアップしました
-
2020.04.01
2020年4月号の記事をアップしました
-
2020.03.16
3月号後半の記事をアップしました
-
2020.03.09
JARD、eラーニングでのアマチュア無線国家資格取得を呼び掛けるお知らせを、臨時休校で自宅待機中の小中高生に向けて発表。詳しくはこちら。
-
2020.03.02
2020年3月号の記事をアップしました
-
2020.02.17
2月号後半の記事をアップしました
-
2020.02.03
2020年2月号の記事をアップしました
-
2020.01.15
1月号後半の記事をアップしました
-
2020.01.06
2020年1月号の記事をアップしました
-
2019.12.16
12月号後半の記事をアップしました
-
2019.12.02
2019年12月号の記事をアップしました
-
2019.11.15
11月号後半の記事をアップしました
-
2019.11.01
2019年11月号の記事をアップしました
-
2019.10.15
10月号後半の記事をアップしました
-
2019.10.01
2019年10月号の記事をアップしました
-
2019.09.17
9月号後半の記事をアップしました
-
2019.09.02
2019年9月号の記事をアップしました
-
2019.08.16
8月号後半の記事をアップしました
-
2019.08.01
2019年8月号の記事をアップしました
-
2019.07.16
7月号後半の記事をアップしました
-
2019.07.01
2019年7月号の記事をアップしました
-
2019.06.17
6月号後半の記事をアップしました
-
2019.06.01
2019年6月号の記事をアップしました
-
2019.05.20
5月号後半の記事をアップしました
-
2019.05.07
2019年5月号の記事をアップしました
-
2019.04.15
4月号後半の記事をアップしました
-
2019.04.01
2019年4月号の記事をアップしました
-
2019.03.15
3月号後半の記事をアップしました
-
2019.03.01
2019年3月号の記事をアップしました
-
2019.02.15
2月号後半の記事をアップしました
-
2019.02.01
2019年2月号の記事をアップしました
-
2019.01.18
1月号後半の記事をアップしました
-
2019.01.07
2019年1月号の記事をアップしました
-
2018.12.17
12月号後半の記事をアップしました
-
2018.12.01
2018年12月号の記事をアップしました
-
2018.11.15
11月号後半の記事をアップしました
-
2018.11.01
2018年11月号の記事をアップしました
-
2018.10.15
10月号後半の記事をアップしました
-
2018.10.01
2018年10月号の記事をアップしました
-
2018.09.15
9月号後半の記事をアップしました
-
2018.09.01
2018年9月号の記事をアップしました
-
2018.08.17
8月号後半の記事をアップしました
-
2018.08.01
2018年8月号の記事をアップしました
-
2018.07.17
7月号後半の記事をアップしました
-
2018.07.02
2018年7月号の記事をアップしました
-
2018.06.15
6月号後半の記事をアップしました
-
2018.06.01
2018年6月号の記事をアップしました
-
2018.05.15
5月号後半の記事をアップしました
-
2018.05.01
2018年5月号の記事をアップしました
-
2018.04.16
4月号後半の記事をアップしました
-
2018.04.02
2018年4月号の記事をアップしました
-
2018.03.15
3月号後半の記事をアップしました
-
2018.03.01
2018年3月号の記事をアップしました
-
2018.02.15
2月号後半の記事をアップしました
-
2018.02.01
2018年2月号の記事をアップしました
-
2018.01.15
1月号後半の記事をアップしました
-
2018.01.05
2018年1月号の記事をアップしました
-
2017.12.15
12月号後半の記事をアップしました
-
2017.12.1
12月号をアップしました
-
2017.11.15
11月号後半の記事をアップしました
-
2017.11.1
11月号をアップしました
-
2017.10.16
10月号後半の記事をアップしました
-
2017.10.2
10月号をアップしました
-
2017.9.15
What a healthy time! ~健康を応援する特別なお料理~/第3回 食物繊維たっぷり! 海藻の和風リゾット、FB Monthly Fashion/第9回 秋っぽい柄&色コーデ、子供の無線教室/第9回 「アンテナの形や大きさに注目!!」を掲載しました
-
2017.9.4
<速報>ハムフェア2017を掲載しました
-
2017.9.1
9月号をアップしました
-
2017.8.17
What a healthy time! ~健康を応援する特別なお料理~/第2回 和風のポトフ 納豆ソース添え、FB Monthly Fashion/第8回 夏のお出かけコーデ、子供の無線教室/第8回 「無線機にはどんなものがあるの?」を掲載しました
-
2017.8.1
8月号をアップしました
-
2017.7.18
What a healthy time! ~健康を応援する特別なお料理~/第1回 メロンの冷製スープ ナッツのアイスクリームのせ、FB Monthly Fashion/第7回 コットンTシャツコーデとボーイズコーデ、子供の無線教室/第7回 「電波はどうやって海外や宇宙に届くの?」を掲載しました
-
2017.7.1
7月号をアップしました
-
2017.6.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第9回 FB Girlsの野望 with ムースと甘エビのタルタル、FB Monthly Fashion/第6回 雨の日コーデと親子コーデ、子供の無線教室/第6回 「電波はいろいろなところで大活躍!!」を掲載しました
-
2017.6.1
6月号をアップしました
-
2017.5.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第8回 番外編 春うらら♪豪華弁当でお花見、FB Monthly Fashion/第5回 ブラウス&シャツを使ったコーディネート、子供の無線教室/第5回 「周波数によって変わる、電波の特徴」を掲載しました
-
2017.5.1
5月号をアップしました
-
2017.4.17
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第7回 ARDFの思い出 with 2種類のソースのカルボナーラ、FB Monthly Fashion/第4回 Gジャンを使ったコーディネート、子供の無線教室/第4回 「電波の性質を覚えよう」を掲載しました
-
2017.4.1
4月号をアップしました
-
2017.3.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第6回 初めてのQSOの思い出 with グリーンのアクアパッツァ、FB Monthly Fashion/第3回 ピンクを使ったコーディネート、子供の無線教室/第3回 「電波はどうやって伝わるの?」を掲載しました
-
2017.3.1
3月号をアップしました
-
2017.2.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第5回 FB Girlsの試験の思い出 withウマ辛和風スープ、FB Monthly Fashion/第2回 デニムと明るめニットのコーディネートを掲載しました
-
2017.2.1
2月号をアップしました
-
2017.1.16
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第4回 YLハムを増やす秘策とは?! withおなかにやさしいお料理、【新連載】FB Monthly Fashion/第1回 アウター別おすすめコーディネート(ライダース・ノーカラー・ダッフル)を掲載しました
-
2017.1.5
1月号をアップしました
-
2016.12.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第3回 YLハムの行く年来る年 with ブイヤベースの洋風お鍋を掲載しました
-
2016.12.1
12月号をアップしました
-
2016.11.15
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(後編)!、What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第2回 YLハムの悩み解決!with サケのフレンチトーストを掲載しました
-
2016.11.1
11月号をアップしました
-
2016.10.17
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(前編)!、【新連載】What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第1回 FB GirlsのプライベートQSO with 土瓶蒸しのリゾットを掲載しました
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)
次号は 12月 1日(木) に公開予定