FBのトレビア
第十六回 サイン、コサインは役に立つ

Dr. FB
令和2年12月期、1アマ、2アマの国家試験の申請書受付は10月1日~20日までです。これから受験しようとされている方はお忘れにならないように。
さて、上級アマチュア無線の受験を経験された方、あるいは今受験勉強中で頑張っておられる方、過去問に下のような問題が出題されています。正弦波交流波形が与えられ、正の半周期の平均、つまり平均値Vaを求めよという問題です。

図1 出典: 日本無線協会HZ008-2 A-5(平成30年8月期A-5)
答えから始めますと、平均値Vaは30Vです。平均値を求める公式は式(1)に記しました。ここで最大値Vmは47Vと題意で与えられていますので、公式に数値を代入すると、平均値は30Vと簡単に算出できます。なお、このA-5の問題の実効値Veと周波数fの解答は末尾に記します。解答にトライしてみてください。

読者の方々、あるいはこれから上級ハムを目指して受験される方々は、平均値Vaは最大値Vmの2/π(≒0.64)と覚えています。「まずは合格にあり」といわれる方々には今回の記事は興味がないかもしれませんが、合格の暁には読み直していただければ幸いです。それではどこから2/πが出てくるのか、今回はその謎の2/πを算出してみます。
平均値とは何か
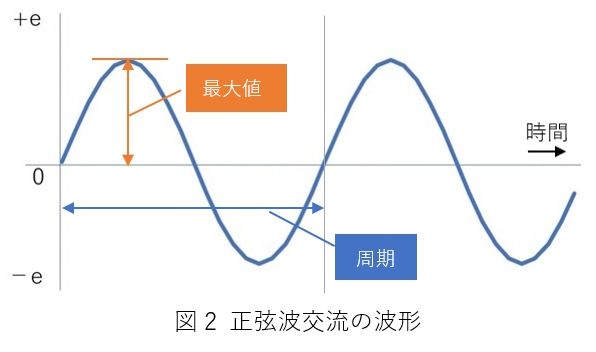
まずは、簡単な復習から始めます。我々の家庭に供給される電力をオシロスコープで観測すると図2のような正弦波交流の波形を見ることができます。オシロスコープで観測できるのは正弦波交流の時間、時間における電圧値と1周期にかかる時間だけです。
試験問題に出題される平均値や実効値がオシロスコープの画面で読めるわけではありません。家庭に供給されているコンセントの電圧も100Vといっていますが、厳密にはオシロスコープの波形を見ると分かるように時間によってその電圧値は異なります。瞬間、瞬間の値、つまり瞬時値は異なりますが、平均はどのくらいかといった電圧はあるはずです。
家のコンセントの電圧の100Vとは何か
さて、家のコンセントの電圧をアナログテスターで測定するとメーターの指示値は100Vです。この値は、実効値です。直流100Vで発生する電力と同じ電力を発生する交流の電圧を実効値100Vといいます。消費電力を計算したり、回路に流れる電流を計算したりする場合に必要な電圧値です。オシロスコープではこの実効値は示されませんが。実効値=最大値÷√2で算出できます。逆に実効値が100Vとすると最大値=実効値×√2=141Vとなります。
家のコンセントの電圧をアナログテスターで測定すると100Vを示しましたが、実はアナログテスターで示される電圧は上がったり下がったりする電圧の平均値なのです。前述しましたが、交流の働きを計算する場合の電圧値は実効値ですから、アナログテスターで表示された平均値の値を約1.1倍して目盛り、それを実効値として使用しています。
平均値を求める
平均値とは、上がったり、下がったりする電圧の平均であると述べました。平均する範囲が図3の0~2πまでとするとS1とS2の平均は「正」の電圧と同じ「負」の電圧を平均するのでゼロとなってしまいます。そこで負の値S2をそのままひっくり返して正の値にします。正負の符号が異なるだけで相似形なので問題はありません。つまりS2の絶対値を取り、S1+|S2|の面積の0~2πまでの平均を取れば平均値を求められます。
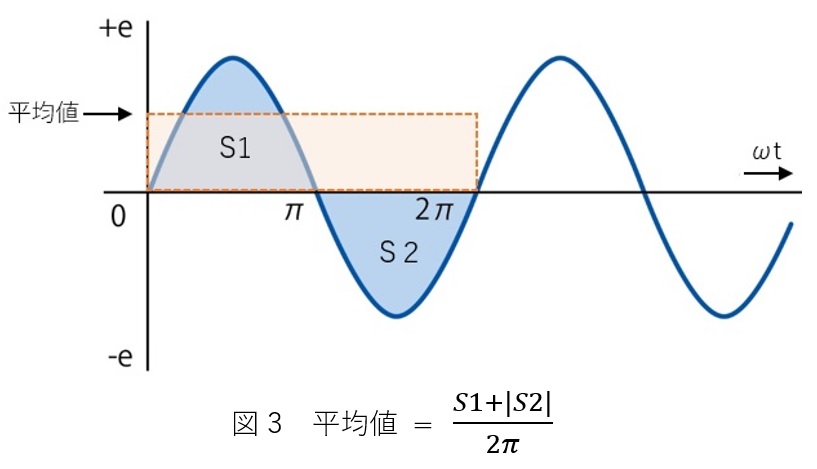
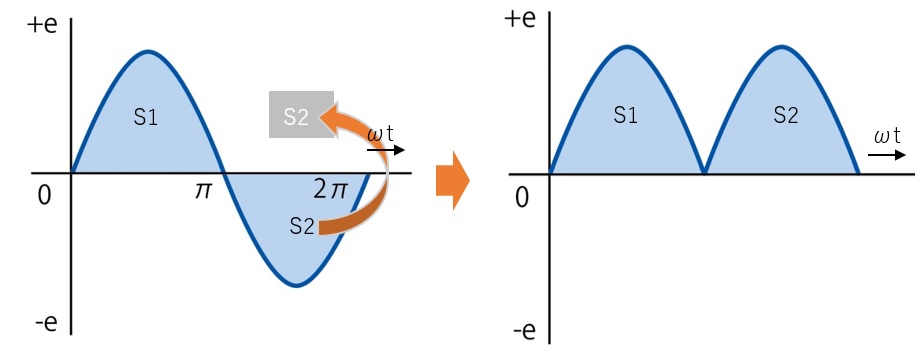
図4 S1+|S2|
図5の正弦波交流の0~2πまでの絶対値の波形を見ると、スタートは0で、その後は徐々に増加し、π/2のポイントで最大となります。その後はπのポイントで再び0となり、これを繰り返します。それではこの増減の平均はどの辺りかとめぼしを付けるとおよそ、図5の破線のあたりぐらいかと推測できます。
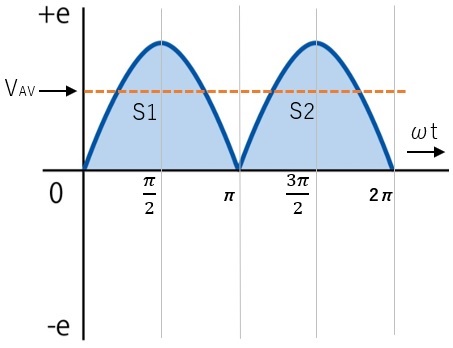
図5 平均値
平均値の求め方
まずS1とS2の合算した面積Sを求めます。これは前述したように1周期分です。面積は縦×横で求められます。つまり求めた面積を底辺(横)の長さで割ると縦の長さとなり、これが平均値VAVとなります。(図6)
ここで図6の波形を見ると分かりますようにS1とS2は同じ波形です。それなら、S1とS2の合計の面積を求めて0~2πで割らなくても、どちらか一つの面積で計算すれば答えは同じことになります。ここではS1の面積を求め、それを底辺の長さで割り算を行い、高さつまり平均値を求めます。
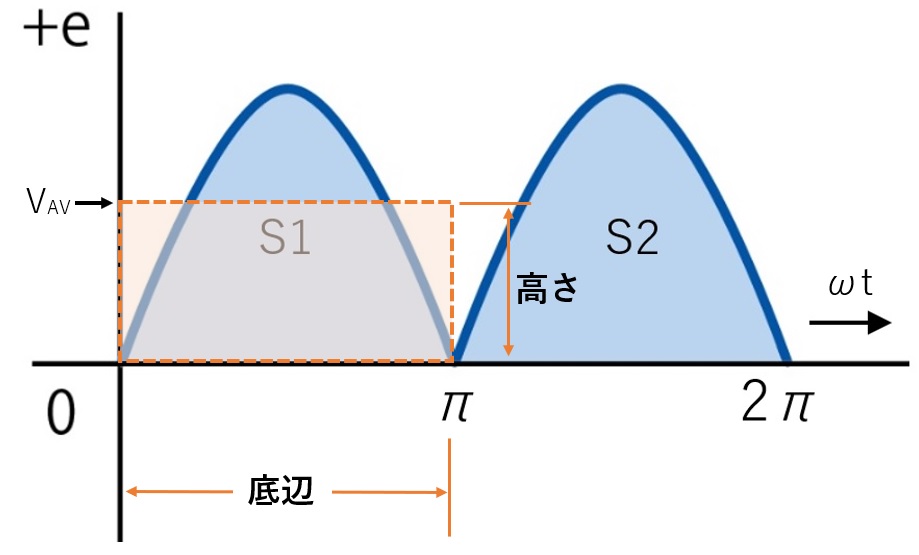
図6 平均値の求め方のシミュレーション
曲線の面積の求め方
さてここでS1の面積を求めますが、一辺が曲線ですので縦×横では単純に面積を求めることはできません。ここは少し難しいですが積分の考え方を用いることにします。(ωt=x)
冒頭の図1は、正弦波交流の波形であると述べました。正弦波は英語でいうとsine waveとなりまさしくy=sin xの波形そのものです。そのy=sin xの波形の0~2πの区間の面積を求める式が下の式(2)です。

今回求めるのはS1の面積ですから、波形の区間は0~πまでです。その区間の面積を定積分で求める式は下の通りです。

式(5)の解は、y=cos xのグラフを描くと分かりやすいかもしれません。図7は、そのy=cos xのグラフです。時間t=π(rad)の時が最小で-1です。時間ωt=0の時はグラフから見ても分かるように最大で+1です。
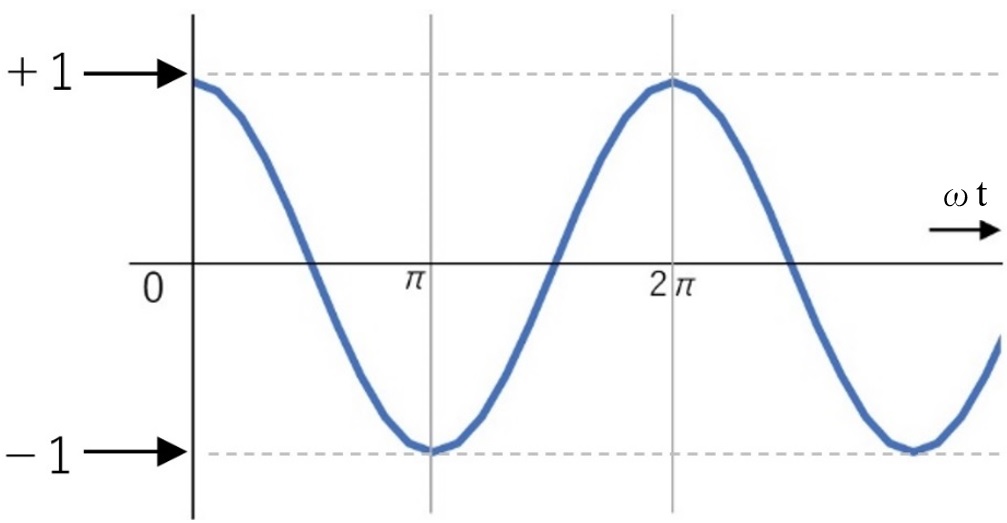
図7 y=cos xのグラフ
面積S1=2と求めることができました。面積S1が分かれば、その面積を横の長さ、図6では底辺の長さで割れば、高さつまり平均値VAVが求まります。この考え方に沿ってもう少し前に進めます。
最後に2/πを算出します
図6のS1の面積が2と算出しました。底辺が同じ長さの四角形を同じ図6に描いています。S1の底辺と四角形の底辺の長さは同じです。つまり面積は縦×横ですから、次の式(7)が成り立ちます。(高さ=VAV、S1=2)

冒頭の平成30年8月期A-5の解答

FBDX
FBのトレビア バックナンバー
- 第四十五回 カウンターICとラダー抵抗によるD/A変換回路でのこぎり波を作る実験
- 第四十四回 ラダー抵抗によるD/A変換について
- 第四十三回 電子ホタルの製作とその解析
- 第四十二回 DCモータの回転数制御について
- 第四十一回 74HC192と74HC4511を使ったアップダウンカウンタの説明
- 第四十回 単電源から正負両電源を作る
- 第三十九回 ホワイトノイズジェネレータでフィルタの特性を見る?
- 第三十八回 ツイストペアケーブルのノイズ軽減は本当か?
- 第三十七回 74HC74を使った分周回路の実験
- 第三十六回 電圧可変抵抗器の考察
- 第三十五回 tinySAで見るひずみ波形のスペクトラム
- 第三十四回 FM放送受信用のQFHアンテナを作ってみた
- 第三十三回 コイルのインダクタンスについて
- 第三十二回 アナログスイッチの動作について
- 第三十一回 小型デジタル電圧計、2線式と3線式は何が違う?
- 第三十回 Back to Backアンテナ、その後の検証
- 第二十九回 オペアンプを使った定電流回路について
- 第二十八回 UHFに対する同軸ケーブルのロス
- 第二十七回 2.4GHz無線LANアンテナ
- 第二十六回 MOSFETを使ってみよう
- 第二十五回 コンパレータについて
- 第二十四回 今さらPLLの原理について
- 第二十三回 MLAの性能をチェック
- 第二十二回 SHF帯のフレネルゾーンについて
- 第二十一回 SGの解放端と負荷端のレベルの差
- 第二十回 Made in Japanは健在か(再び変換コネクター)
- 第十九回 Back to Backアンテナの実用の可能性
- 第十八回 SWR測定、アンテナ直下がベストは本当だった
- 第十七回 受信感度低下の正体はBNC L型コネクターか
- 第十六回 サイン、コサインは役に立つ
- 第十五回 BIRD 43はほんとうに正確か
- 第十四回 ダイポールアンテナにバランは必要か
- 第十三回 ゲルマニウムラジオは何故シリコンラジオと呼ばれないか?
- 第十二回 7セグメントLEDの点灯
- 第十一回 ハンディー機のアンテナSWRと送受信の相関を検証 (その3)
- 第十回 ハンディー機のアンテナSWRの測定(その2)
- 第九回 ハンディー機のアンテナSWRの測定(その1)
- 第八回 CM形電力計
- 第七回 V/UHF帯3バンドアンテナ解体新書
- 第六回 トリプレクサーってなんだ
- 第五回 アナログメーターのちょっと変わったスペック
- 第四回 50Ω不平衡ってなんのこと
- 第三回 マルチバンドアンテナのトラップのお話
- 第二回 dBm(デービーエム)のお話
- 第一回 dB(デシベル)のお話
お知らせ
-
2022.11.15
11月号後半の記事をアップしました
-
2022.11.1
11月号の記事をアップしました
-
2022.10.17
10月号後半の記事をアップしました
-
2022.10.3
10月号の記事をアップしました
-
2022.9.15
9月号後半の記事をアップしました
-
2022.9.1
9月号の記事をアップしました
-
2022.8.15
8月号後半の記事をアップしました
-
2022.8.1
8月号の記事をアップしました
-
2022.7.15
7月号後半の記事をアップしました
-
2022.7.1
7月号の記事をアップしました
-
2022.6.15
6月号後半の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JL3ZGL」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2022.6.1
6月号の記事をアップしました
6月4日(土)、JH1CBX/3が14MHz SSBに初オンエアします。 入感がありましたらぜひお声がけください。 -
2022.5.16
5月号後半の記事をアップしました
-
2022.5.2
5月号の記事をアップしました
5月14日(土)、JL3ZGLはオペレーターにMasacoさんを迎えHAMtte交信パーティに 参加します。詳しくは4月号のニュースをご確認ください。 -
2022.4.15
4月号後半の記事をアップしました
-
2022.4.1
4月号の記事をアップしました
-
2022.3.15
3月号後半の記事をアップしました
-
2022.3.1
3月号の記事をアップしました
-
2022.2.15
2月号後半の記事をアップしました
-
2022.2.1
2月号の記事をアップしました
-
2022.1.17
1月号後半の記事をアップしました
-
2022.1.5
1月号の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JA3YUA」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2021.12.15
12月号後半の記事をアップしました
-
2021.12.1
12月号の記事をアップしました
-
2021.11.15
11月号後半の記事をアップしました
-
2021.11.01
2021年11月号の記事をアップしました
-
2021.10.15
10月号後半の記事をアップしました
-
2021.10.01
2021年10月号の記事をアップしました
-
2021.09.15
9月号後半の記事をアップしました
-
2021.09.01
2021年9月号の記事をアップしました
-
2021.08.16
8月号後半の記事をアップしました
-
2021.08.02
2021年8月号の記事をアップしました
-
2021.07.15
7月号後半の記事をアップしました
-
2021.07.01
2021年7月号の記事をアップしました
-
2021.06.15
6月号後半の記事をアップしました
-
2021.06.01
2021年6月号の記事をアップしました
-
2021.05.17
5月号後半の記事をアップしました
-
2021.05.06
2021年5月号の記事をアップしました
-
2021.04.15
4月号後半の記事をアップしました
-
2021.04.01
2021年4月号の記事をアップしました
連載記事 Masacoの「むせんのせかい」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.15
3月号後半の記事をアップしました
連載記事「今月のハム」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.01
2021年3月号の記事をアップしました
-
2021.02.15
2月号後半の記事をアップしました
-
2021.02.01
2021年2月号の記事をアップしました
-
2021.01.15
1月号後半の記事をアップしました
-
2021.01.05
2021年1月号の記事をアップしました
-
2020.12.15
12月号後半の記事をアップしました
-
2020.12.01
2020年12月号の記事をアップしました
-
2020.11.16
11月号後半の記事をアップしました
-
2020.11.02
2020年11月号の記事をアップしました
-
2020.10.15
10月号後半の記事をアップしました
-
2020.10.01
2020年10月号の記事をアップしました
-
2020.09.15
9月号後半の記事をアップしました
-
2020.09.01
2020年9月号の記事をアップしました
-
2020.08.17
8月号後半の記事をアップしました
-
2020.08.03
2020年8月号の記事をアップしました
-
2020.07.15
7月号後半の記事をアップしました
-
2020.07.01
2020年7月号の記事をアップしました
-
2020.06.15
6月号後半の記事をアップしました
-
2020.06.01
2020年6月号の記事をアップしました
-
2020.05.01
2020年5月号の記事をアップしました
-
2020.04.15
4月号後半の記事をアップしました
-
2020.04.01
2020年4月号の記事をアップしました
-
2020.03.16
3月号後半の記事をアップしました
-
2020.03.09
JARD、eラーニングでのアマチュア無線国家資格取得を呼び掛けるお知らせを、臨時休校で自宅待機中の小中高生に向けて発表。詳しくはこちら。
-
2020.03.02
2020年3月号の記事をアップしました
-
2020.02.17
2月号後半の記事をアップしました
-
2020.02.03
2020年2月号の記事をアップしました
-
2020.01.15
1月号後半の記事をアップしました
-
2020.01.06
2020年1月号の記事をアップしました
-
2019.12.16
12月号後半の記事をアップしました
-
2019.12.02
2019年12月号の記事をアップしました
-
2019.11.15
11月号後半の記事をアップしました
-
2019.11.01
2019年11月号の記事をアップしました
-
2019.10.15
10月号後半の記事をアップしました
-
2019.10.01
2019年10月号の記事をアップしました
-
2019.09.17
9月号後半の記事をアップしました
-
2019.09.02
2019年9月号の記事をアップしました
-
2019.08.16
8月号後半の記事をアップしました
-
2019.08.01
2019年8月号の記事をアップしました
-
2019.07.16
7月号後半の記事をアップしました
-
2019.07.01
2019年7月号の記事をアップしました
-
2019.06.17
6月号後半の記事をアップしました
-
2019.06.01
2019年6月号の記事をアップしました
-
2019.05.20
5月号後半の記事をアップしました
-
2019.05.07
2019年5月号の記事をアップしました
-
2019.04.15
4月号後半の記事をアップしました
-
2019.04.01
2019年4月号の記事をアップしました
-
2019.03.15
3月号後半の記事をアップしました
-
2019.03.01
2019年3月号の記事をアップしました
-
2019.02.15
2月号後半の記事をアップしました
-
2019.02.01
2019年2月号の記事をアップしました
-
2019.01.18
1月号後半の記事をアップしました
-
2019.01.07
2019年1月号の記事をアップしました
-
2018.12.17
12月号後半の記事をアップしました
-
2018.12.01
2018年12月号の記事をアップしました
-
2018.11.15
11月号後半の記事をアップしました
-
2018.11.01
2018年11月号の記事をアップしました
-
2018.10.15
10月号後半の記事をアップしました
-
2018.10.01
2018年10月号の記事をアップしました
-
2018.09.15
9月号後半の記事をアップしました
-
2018.09.01
2018年9月号の記事をアップしました
-
2018.08.17
8月号後半の記事をアップしました
-
2018.08.01
2018年8月号の記事をアップしました
-
2018.07.17
7月号後半の記事をアップしました
-
2018.07.02
2018年7月号の記事をアップしました
-
2018.06.15
6月号後半の記事をアップしました
-
2018.06.01
2018年6月号の記事をアップしました
-
2018.05.15
5月号後半の記事をアップしました
-
2018.05.01
2018年5月号の記事をアップしました
-
2018.04.16
4月号後半の記事をアップしました
-
2018.04.02
2018年4月号の記事をアップしました
-
2018.03.15
3月号後半の記事をアップしました
-
2018.03.01
2018年3月号の記事をアップしました
-
2018.02.15
2月号後半の記事をアップしました
-
2018.02.01
2018年2月号の記事をアップしました
-
2018.01.15
1月号後半の記事をアップしました
-
2018.01.05
2018年1月号の記事をアップしました
-
2017.12.15
12月号後半の記事をアップしました
-
2017.12.1
12月号をアップしました
-
2017.11.15
11月号後半の記事をアップしました
-
2017.11.1
11月号をアップしました
-
2017.10.16
10月号後半の記事をアップしました
-
2017.10.2
10月号をアップしました
-
2017.9.15
What a healthy time! ~健康を応援する特別なお料理~/第3回 食物繊維たっぷり! 海藻の和風リゾット、FB Monthly Fashion/第9回 秋っぽい柄&色コーデ、子供の無線教室/第9回 「アンテナの形や大きさに注目!!」を掲載しました
-
2017.9.4
<速報>ハムフェア2017を掲載しました
-
2017.9.1
9月号をアップしました
-
2017.8.17
What a healthy time! ~健康を応援する特別なお料理~/第2回 和風のポトフ 納豆ソース添え、FB Monthly Fashion/第8回 夏のお出かけコーデ、子供の無線教室/第8回 「無線機にはどんなものがあるの?」を掲載しました
-
2017.8.1
8月号をアップしました
-
2017.7.18
What a healthy time! ~健康を応援する特別なお料理~/第1回 メロンの冷製スープ ナッツのアイスクリームのせ、FB Monthly Fashion/第7回 コットンTシャツコーデとボーイズコーデ、子供の無線教室/第7回 「電波はどうやって海外や宇宙に届くの?」を掲載しました
-
2017.7.1
7月号をアップしました
-
2017.6.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第9回 FB Girlsの野望 with ムースと甘エビのタルタル、FB Monthly Fashion/第6回 雨の日コーデと親子コーデ、子供の無線教室/第6回 「電波はいろいろなところで大活躍!!」を掲載しました
-
2017.6.1
6月号をアップしました
-
2017.5.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第8回 番外編 春うらら♪豪華弁当でお花見、FB Monthly Fashion/第5回 ブラウス&シャツを使ったコーディネート、子供の無線教室/第5回 「周波数によって変わる、電波の特徴」を掲載しました
-
2017.5.1
5月号をアップしました
-
2017.4.17
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第7回 ARDFの思い出 with 2種類のソースのカルボナーラ、FB Monthly Fashion/第4回 Gジャンを使ったコーディネート、子供の無線教室/第4回 「電波の性質を覚えよう」を掲載しました
-
2017.4.1
4月号をアップしました
-
2017.3.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第6回 初めてのQSOの思い出 with グリーンのアクアパッツァ、FB Monthly Fashion/第3回 ピンクを使ったコーディネート、子供の無線教室/第3回 「電波はどうやって伝わるの?」を掲載しました
-
2017.3.1
3月号をアップしました
-
2017.2.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第5回 FB Girlsの試験の思い出 withウマ辛和風スープ、FB Monthly Fashion/第2回 デニムと明るめニットのコーディネートを掲載しました
-
2017.2.1
2月号をアップしました
-
2017.1.16
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第4回 YLハムを増やす秘策とは?! withおなかにやさしいお料理、【新連載】FB Monthly Fashion/第1回 アウター別おすすめコーディネート(ライダース・ノーカラー・ダッフル)を掲載しました
-
2017.1.5
1月号をアップしました
-
2016.12.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第3回 YLハムの行く年来る年 with ブイヤベースの洋風お鍋を掲載しました
-
2016.12.1
12月号をアップしました
-
2016.11.15
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(後編)!、What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第2回 YLハムの悩み解決!with サケのフレンチトーストを掲載しました
-
2016.11.1
11月号をアップしました
-
2016.10.17
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(前編)!、【新連載】What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第1回 FB GirlsのプライベートQSO with 土瓶蒸しのリゾットを掲載しました
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)
次号は 12月 1日(木) に公開予定