A famous measuring instrument (Impedance Bridge) of the past in Japan

If the capacitance of a capacitor and the inductance of a coil are known, the resonant frequency can be obtained by a formula. Most capacitors have the capacitance printed on the surface of their components, but coils are often made by hand, which annoys the homebrewers. So, I will try to build a simple inductance meter to measure the inductance of coils. Although it is not as accurate as a commercially available measuring device with a digital display, I aim to build it as usable as possible.

In Part 1 of this issue, I will briefly explain the principle of the building process, and in Part 2, I will actually start the building process and put it in a plastic case.

How to find the inductance of a coil

Let us consider how to find the inductance of a coil. Figure 1 shows a method using an AC bridge. When the AC bridge is balanced, the equation 2πfLx ×R2 = 2πfL1×R1 holds. At this time, the potentials at both ends of G (galvanometer) are equal, so no current flows through G. This method is used to find the inductance of Lx by searching for this state of no current flow.

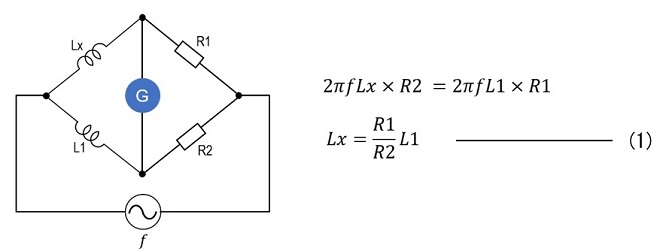
Figure 1. Method using an AC bridge

Connect an unknown coil Lx, L1 of known value, and the variable resistors R1 and R2 as shown in Figure 1. Once the circuit is balanced, Lx can be obtained from equation (1) above. In other words, Lx is the value of R1/R2 with the circuit multiplied by the value of L1.

Preliminary experiments with this circuit did not work well. The reason may be that the equation (1) in Figure 1 does not include a frequency parameter, so I set the frequency to the MHz range without considering the frequency to be used. Also, the high-frequency characteristics of the variable resistors R1 and R2 may have been poor. If ƒ in a signal oscillator is set to a lower frequency, the R1 and R2 frequency characteristics may be negligible, but I did not conduct any subsequent experiments.

Equation (2) below is the formula for finding the resonant frequency of the LC circuit. Figure 2 shows a circuit containing an LC resonant circuit. When a parallel resonant circuit of Lx and C resonates for an AC signal of ƒ Hz, the impedance of the resonant circuit becomes very high and current does not flow in the resonant circuit but flows mostly in the load R side.

Therefore, the swing of the ammeter (A) connected in series with the load is at its maximum. Such an LC parallel resonance circuit can be seen in many high-frequency circuits such as transmitters and receivers. Since they are relatively easy to make, I will use this principle to build the inductance meter.

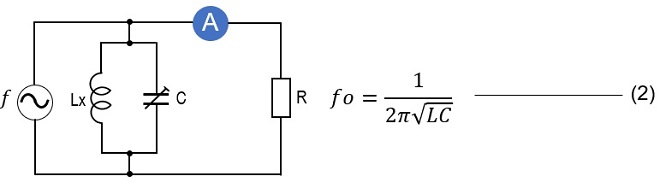
Figure 2. Method using LC resonance circuit

Block Diagram of the Inductance Meter to be built

Figure 3 shows a block diagram of the simple inductance meter using an LC parallel resonance circuit. It consists mainly of the four blocks shown below.
(1) Oscillation circuit
(2) Tuning circuit
(3) Meter drive circuit
(4) Display circuit

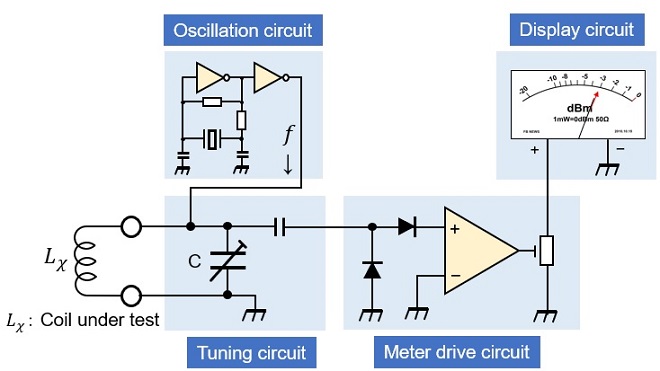
Figure 3. Block diagram of inductance meter

Principle of the inductance meter to be manufactured

Lx in Figure 3 is the inductance (coil) to be measured. The tuning circuit (parallel resonance circuit) is created by connecting a variable capacitor in parallel with the coil. The parallel resonant circuit has a unique resonant frequency (ƒ₀) at the values of Lx and C. The impedance of the parallel circuit at this resonant frequency (ƒ₀) is very high and maximum, as shown in Figure 4, but the impedance is low at frequencies other than the resonant frequency. In other words, the characteristic that current is difficult to flow when the impedance is high and current flows well when the impedance is low is utilized.

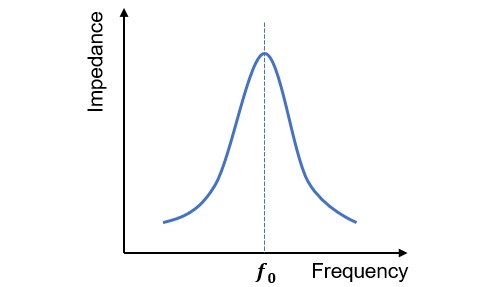
Figure 4. Relationship between frequency and impedance in a parallel resonant circuit

The AC signal created by the oscillation circuit in Figure 3 is added to the tuning circuit. If the circuit is not resonant at the frequency of that signal, the impedance of the tuned circuit is low, and the AC signal flows through Lx and C to ground.

Since C is a variable capacitor, varying the capacitance changes the resonant frequency of the tuning circuit of Lx and C. By varying the capacitance of C, the resonant frequency of the circuit is matched to the frequency of the AC signal at ƒ Hz. At this time, the impedance of the circuit becomes very high, and the circuit is said to be resonate with respect to the AC signal because of the high impedance of the circuit. The AC signal does not flow to ground through Lx and C but flows into the meter drive circuit through a rectifier circuit composed of diodes. The drive circuit amplifies the signal to make the meter swing.

If the value of capacitance C when the meter swings to its maximum is known, the inductance of the coil can be obtained from formula (1) in Figure 5.

Calculating the measurement range of inductance

Equation (1) in Figure 5 is a formula for finding the resonance frequency (ƒ₀). If the values of L and C are known, the resonance frequency (ƒ₀) can be easily obtained by substituting the respective values. Formula (4) in Figure 5 is a variant of Formula (1) in Figure 5 to obtain inductance (L).

Equation (4) in Figure 5 shows that C and L are inversely proportional to each other. It also shows that they are inversely proportional to the square of the frequency. If the oscillation frequency ƒ₀ = 10 MHz and the variable range of the variable capacitor is C = 10 to 250 pF, and if each value is substituted into the equation (4) in Figure 5, the measurable inductance can be calculated to be 1 µH to 25 µH. This is too narrow a measurement range. To expand the inductance measurement range from µH to mH, either lower the capacitance C of the variable capacitor more or lower the oscillation frequency (ƒ₀) more.

Figure 5. Formula for finding resonance frequency

Preparations

The measurement range of the inductance meter to be built is assumed to be from µH to mH. As mentioned above, if the oscillation frequency ƒ₀ = 10 MHz and the variable capacitor range of C is 10 pF to 250 pF, the measurement range is 1 µH to 25 µH based on formula (4) in Figure 5.

Therefore, I will use a lower oscillation frequency. As I had a 10 MHz crystal on hand, I used it in a logic circuit using a D-FF (D-flipflop) (refer to the Technical Trivia by Dr. FB for the September 2022 issue of the monthly FB news) to create 1.25 MHz by repeating 1/2 frequency division 3 times. In this way, the calculated value can be measured down to 1600 µH (=1.6 mH).

Figure 6 shows the relationship between the capacitance of the variable capacitor and the inductance that can be measured with respect to the oscillation frequency. Based on this, we will go on to the fabrication in the next issue.

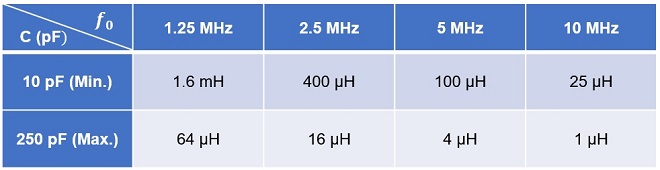
Figure 6. Calculated values of the measurement range of inductance against oscillation frequency and capacitance of the variable capacitor.

CU