Mr. Smithとインピーダンスマッチングの話
【第35話】 アンテナと空間のインピーダンス(その3 放射電力と空間のインピーダンス)
第34話ではダイポールアンテナを例にとり、実際に所望の電力の電磁波を発生させる方法について解説しました。電力P[W]の電磁波を空間に放射するためには、アンテナの放射抵抗RrにP[W]の電力を消費させる・・・ すなわち、Rrに [A]の電流を流す必要があります。
第35話では、放射抵抗Rrの大きさはどうやって決定されるのかの解説に先立ち、アンテナに給電されたP[W]の電力は空間にどのように輻射されるのかについて解説します。
1. 微小ダイポール(電流ダイポール)が発生する電磁波
図1は第33話の図3の再掲です。電磁波は電流の振動(交流電流)を波源とし、電界Eと磁界Hの振動が波として伝播するものでした。
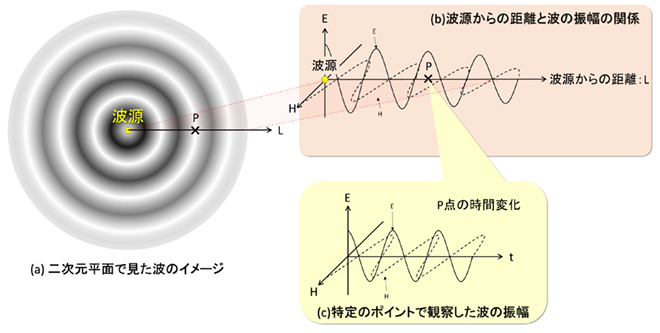
図1 電磁波のイメージ図(第33話の再掲)
実際には、アンテナから放射される電磁波は2次元平面ではなく3次元空間に広がります。従って、図1を図2に置き換えて考える事とします。
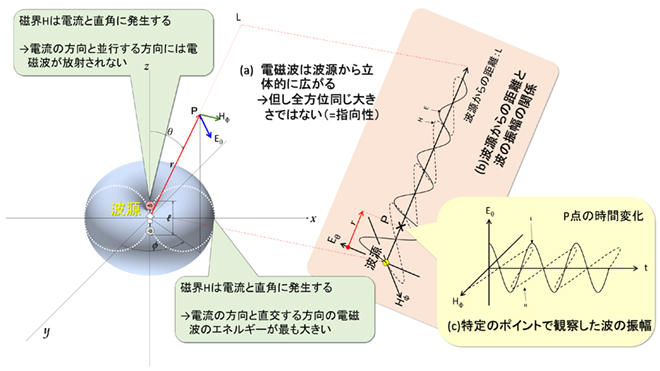
図2 3次元空間で考えた電磁波のイメージ図(波源が電流ダイポールの場合)
3次元の空間において、電磁波は全方向に一様に広がってゆきますが、波源の電流ダイポールには、1次元の方向性(電流の流れる方向)があり、磁界Hは電流I と直交する方向に発生するため、電流と直角の方向に最も強く放射する一方、電流と並行する方向には発生しません。この結果、図2に示すように電磁波の等電力面(等しい電力値を結んだ面)は球面とはならず、電流方向がへこんだドーナツのような形状になります※1。3Dの挿絵がイマイチなので平面図(図3)も参照ください。このように方位角によって電波の放射強度が変化する特性を「指向性」と呼びます。電磁波の波源は電流であるため、球面状(どの方向にも同じ強さ)に電磁波を放射することはできませんが、伝播は球面状に一様です。従って、図2に示したドーナツ型のまま広がってゆく事になります。半波長ダイポールアンテナにおいても定性的には同じです※2。
※1:図2、図5の青いドーナツ形状は電界強度(磁界強度)分布を示すイメージであって、本来は3次元空間の距離座標を示す本図に一緒に記載すべきものではありません。便宜上の表現であることをご了承ください。正確には3次元強度分布を示す図3を参照ください。
※2:電流ダイポールの場合は図2における区間ℓ の電流が一様分布ですが、半波長ダイポールアンテナでは電流がコサイン関数になるため、同じドーナツ形状(8の字特性)でも同一にはなりません。
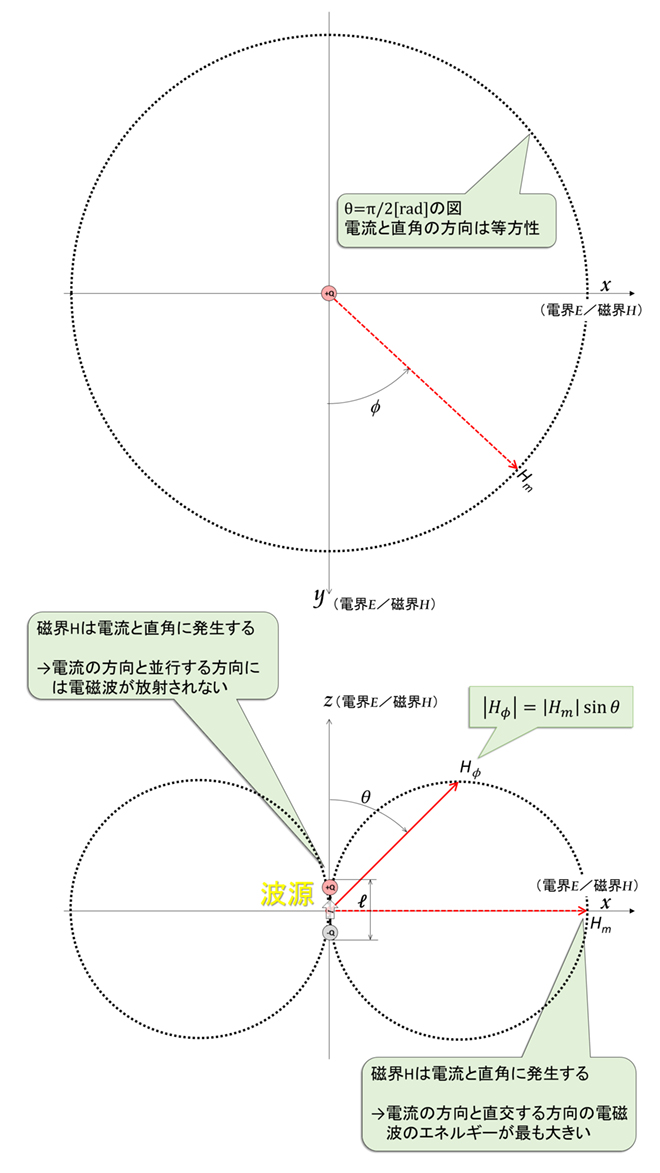
図3 電流ダイポールの指向性(グラフの軸が電磁界強度であることに注意)
2. 電磁波の電力
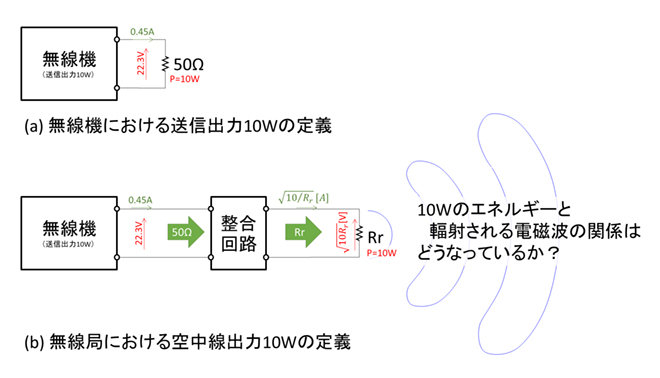
無線機の出力電力とは所定の負荷抵抗(一般的には50Ω)を接続した時に、その抵抗で消費される電力の平均値(送信期間中の平均値)を示します。図4(a)は送信出力10Wの無線機の送信出力の定義を示したものです。電波を放射するためには、これにアンテナ(空中線)を接続するのですが、第34話で示した通り、アンテナの放射抵抗Rrは50Ωではないので、何らかの整合回路を介します(図4(b))。結果、アンテナには10Wの高周波電力が給電されることになります。電波法ではこの電力を「空中線電力」と呼んでいます。
等価回路的にはこれで解った気になるのですが、さてアンテナに給電された10Wの電力は空間にどのように輻射されるのでしょうか。引き続き図2の微小ダイポールに10Wの電力を給電したとして考察します(Rrが小さく、大きな容量性リアクタンスが存在しますが、整合回路で整合できた前提です)。アンテナに供給された10Wのエネルギーは図2に示したドーナツ型の形状で空間に広がってゆきますが、空間に雨や遮蔽物など何もなければ電磁波の総エネルギーは広がるだけで減衰しません。つまり波源から半径rの球面(図5参照)を考えた時に球面上の電力を全て積分する(足し合わせる)と10Wになります。別の見方をすると球の表面積は4πr2なので、10Wの波源から距離rだけ離れた場所における平均の電力密度Pravrは、
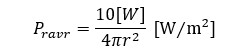
(式2-1)
となりrの2乗に比例して小さく(薄く)なります。これを自由空間における伝搬損失と呼んでいますが、「損失」というにはちょっとイメージが合わないかもしれません。
実際には1章で述べた通り、電流ダイポールの放射する電磁波には指向性があるので、波源からある方向にrだけ離れた点P
での電力密度Prはθ,ϕ の関数となり、
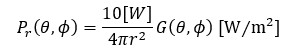
(式2-2)
となります。ここでG(θ,ϕ )は波源からP点の方向のアンテナ利得(指向性利得)を示します。アンテナ利得については次号以降で解説します。これらの式からわかるように、波源から半径rの球面上の電力密度を球面全体に渡って積分すると、アンテナに供給された電力(=10W)になります。
3. 電磁波の電力と電界・磁界の関係
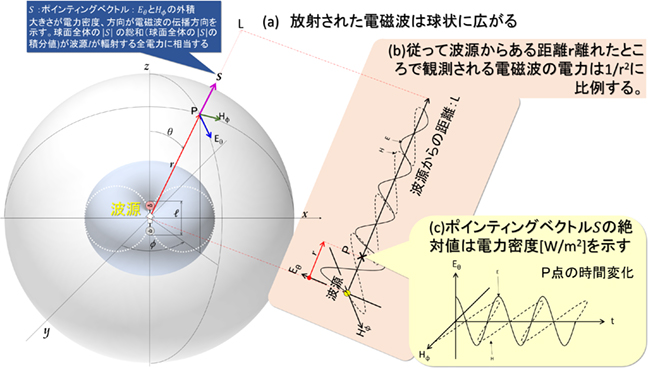
次に電磁波の電力と電界・磁界の振幅の関係を考察します。2章までは電界強度E、磁界強度H、電力密度Prとしてスカラー量的に取り扱ってきましたが、電界も磁界も電力密度も図5に示すようにベクトル量なので大きさだけではなく方向を持った値です。
2章ではPrというスカラー量で説明しましたが、波源から半径rの球面を仮定したときの、その表面上の電力密度ベクトルS [W/m2]をポインティングベクトルと言います。|S |を球の表面全体に渡って積分すると波源が放射する電力値=アンテナへの給電電力になるのは先程述べたとおりです。ポインティングベクトルS は(式3-1)に示す通り、電界ベクトルE 、磁界ベクトルH の外積で導出されるベクトルであり、大きさは電力密度、方向は電磁波の進行方向を示します。
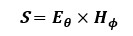
(式3-1)
なお電界ベクトルE の添え字θ
と磁界ベクトルH の添え字ϕ は、それぞれ極座標で示した電界ベクトルのθ
軸成分と磁界ベクトルのϕ 軸成分を示しています。電流ダイポールがz軸と並行である限りEϕ 成分、Hθ
成分は生じません。
また(式3-1)から、波源からある方向に距離r離れた点Pでの電力密度Prは
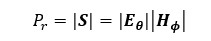
(式3-2)
となります。
4. 空間のインピーダンス
電磁波の電力(電力密度)Pr[W/m2]が電界E [V/m]と磁界H [A/m]の積になることはお判り頂けたと思います。波源は電流ダイポールなので、電流値I [A]※3から磁界の大きさH を導出することは可能ですが、電界の大きさE はどうすれば求められるのでしょうか。
実は媒質中を伝播する電磁波の電界E と磁界H の振幅比は媒質の誘電率と透磁率で決まってしまい、どちらかが決まると他方は一意に決まってしまいます。このことは真空中でも同じで、真空中におけるE とH の比η は、
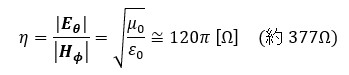
ε0:真空誘電率≅8.85×10-12[F/m]
μ0:真空透磁率≅1.26×10-6[N/A-2]
(式4-1)
で与えられます。なお、120πと書くと空間のインピーダンスは何か幾何学的に導出できる数値のように思ってしまいますが、この値は実験から導出された値を120πに近似したものあって、幾何学的に導出された値ではありません。単位がΩとなっているのでお気づきと思いますが、電界と磁界の比は[V/m]と[A/m]の比なので、インピーダンスの次元をもった諸元となり、これを空間のインピーダンスと呼びます。
古い話ですが、似たような話が第4話で登場したのを覚えておられるでしょうか。図6は第4話の図5を再掲したものです。赤線で囲った箇所は伝送線路の特性インピーダンスが単位長あたりのインダクタンスとキャパシタンスの比の平方根になる事を示していますが、インダクタンスは透磁率μで、キャパシタンスは誘電率εでそれぞれ決定されるので、実は同じ事を示しています。
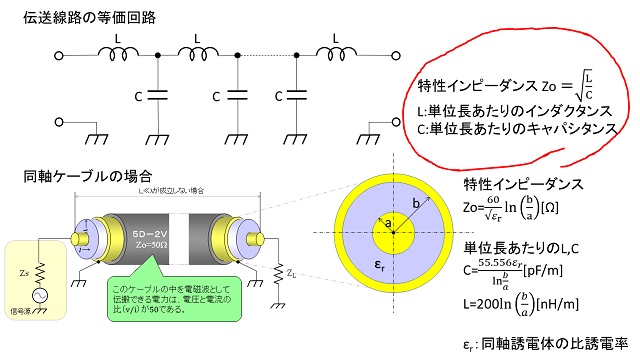
図6 伝送線路の特性インピーダンス(第4話から再掲)
つまり、伝送線路でも真空中でも電力が電磁波として伝播する際は、伝播できる電界と磁界の振幅比率が決まっており、それを示しているのが固有インピーダンスη
です。η
は伝送線路でいうZ0に該当し、空間の特性インピーダンスZ0とも表現されます。
従って、波源であるI [A]の電流(電流ダイポール)※3から発生する磁界H の大きさが判れば、ある方向に輻射される電磁波の電界ベクトルE と電力密度ベクトルPr の大きさは、それぞれ
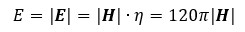
(式4-2)
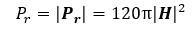
(式4-3)
の関係となります。
※3:正確には電流変化の大きさです。(直流電流から電磁波は発生しません)
5. 第35話のまとめ
これで電磁波の電力とアンテナに流れる電流の関係が整理できました。一般論としてアンテナに流れる電流の大きさと分布が決まれば、マクスウェルの方程式から距離rの位置における磁界の大きさ|H |が導出できます(まだ解説していません)。磁界の大きさがわかれば(式4-2)(式4-3)の関係を用いてアンテナからある方向に輻射される電力が判るので、この計算をアンテナの周囲全体に対して行い、アンテナが輻射した総電力が判れば、総電力と電流からアンテナの放射抵抗Rrが決まるのですが、このあたりの話は次回とさせてください。以下、第35話の要点を整理します。
(1) 電流ダイポールから輻射される電磁波は完全等方性にはならず、電流と直交する方向に最も強く、並行する方向には輻射されないドーナツ状の強度分布(指向性)を示す。
(2) 自由空間においては、輻射された電磁波は球面状に広がって伝播するので、波源(アンテナ)から見た電磁波は(1)の強度分布を維持して広がってゆく。
(3) アンテナから距離r離れた点の電磁波の電力密度ベクトルS は電界E と磁界H の外積となる。
(4) 波源(アンテナ)を囲む球面上で電力密度ベクトルの絶対値|S |(=Pr)を積分した結果はアンテナへの給電電力(空中線電力)と等しくなる。
(5) 真空中(自由空間)には固有インピーダンスη が存在し、電界の大きさと磁界の大きさの比がη となる電磁波以外は伝播することができない。従ってEまたはHのどちらかが判明すれば、電力密度Prはη を使って導出することが可能である。
(6) 真空中(自由空間)の固有インピーダンスη は約120π[Ω]であることが経験的に知られている。
次回はアンテナの放射抵抗Rrの導出について解説します。
【参考文献】
(1) アンテナ入門 F.R.Conner 原著 安藤真 訳 森北出版 1990年
(2) 電磁波とは何か 後藤尚久 著 講談社 1984年
(3) ANTENNAS Second Edition J.D.KRAUS McGRAW-HILL 1988年
Mr. Smithとインピーダンスマッチングの話 バックナンバー
- 【第40話】 (連載最終話) インピーダンスマッチングの四方山話
- 【第39話】 アンテナと空間のインピーダンス(その6 平衡と不平衡(その2))
- 【第38話】 アンテナと空間のインピーダンス(その6 平衡と不平衡(その1))
- 【第37話】 アンテナと空間のインピーダンス(その5 放射抵抗と給電抵抗)
- 【第36話】 アンテナと空間のインピーダンス(その4 アンテナの放射抵抗)
- 【第35話】 アンテナと空間のインピーダンス(その3 放射電力と空間のインピーダンス)
- 【第34話】 アンテナと空間のインピーダンス(その2 ダイポールアンテナ)
- 【第33話】 アンテナと空間のインピーダンス(その1 電磁波とは何か)
- 【第32話】 低雑音増幅器(LNA)のインピーダンスマッチング(その7・LNAの設計(後編))
- 【第31話】 低雑音増幅器(LNA)のインピーダンスマッチング(その6・LNAの設計 (前編))
- 【第30話】 低雑音増幅器(LNA)のインピーダンスマッチング(その5・定NF円)
- 【第29話】 低雑音増幅器(LNA)のインピーダンスマッチング(その4・ノイズパラメータ)
- 【第28話】 低雑音増幅器(LNA)のインピーダンスマッチング(その3・NFマッチ)
- 【第27話】 低雑音増幅器(LNA)のインピーダンスマッチング(その2・NFとSN比)
- 【第26話】 低雑音増幅器(LNA)のインピーダンスマッチング(その1・雑音とは何か)
- 【第25話】 そのインピーダンス、本当に存在しますか? (その2)
- 【第24話】 そのインピーダンス、本当に存在しますか? (その1)
- 【第23話】 トランジスタの利得とミスマッチの関係
- 【第22話】 トランジスタの出力インピーダンスと負荷インピーダンス
- 【第21話】 S12と付き合う(その3)
- 【第20話】 S12と付き合う(その2)
- 【第19話】 S12と付き合う(その1)
- 【第18話】 S12の正体
- 【第17話】 増幅器とSパラメータ(その2)
- 【第16話】 増幅器とSパラメータ(その1)
- 【第15話】 Qとは何か(その3)
- 【第14話】 Qとは何か(その2)
- 【第13話】 Qとは何か(その1)
- 【第12話】 λ/4線路の共振と分布定数回路(その2)
- 【第11話】 λ/4線路の共振と分布定数回路(その1)
- 【第10話】 Sパラメータの基礎
- 【第9話】 直列共振と並列共振 その2
- 【第8話】 直列共振と並列共振
- 【第7話】 スミスチャートは日本人の発明?
- 【第6話】 スミスチャートとは何か(その2)
- 【第5話】 伝送線路と反射係数(その2)
- 【第4話】 伝送線路と反射係数
- 【第3話】 スミスチャートとは何か(その1)
- 【第2話】 インピーダンスマッチングの方法
- 【第1話】 なぜインピーダンスマッチング?
お知らせ
-
2022.11.15
11月号後半の記事をアップしました
-
2022.11.1
11月号の記事をアップしました
-
2022.10.17
10月号後半の記事をアップしました
-
2022.10.3
10月号の記事をアップしました
-
2022.9.15
9月号後半の記事をアップしました
-
2022.9.1
9月号の記事をアップしました
-
2022.8.15
8月号後半の記事をアップしました
-
2022.8.1
8月号の記事をアップしました
-
2022.7.15
7月号後半の記事をアップしました
-
2022.7.1
7月号の記事をアップしました
-
2022.6.15
6月号後半の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JL3ZGL」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2022.6.1
6月号の記事をアップしました
6月4日(土)、JH1CBX/3が14MHz SSBに初オンエアします。 入感がありましたらぜひお声がけください。 -
2022.5.16
5月号後半の記事をアップしました
-
2022.5.2
5月号の記事をアップしました
5月14日(土)、JL3ZGLはオペレーターにMasacoさんを迎えHAMtte交信パーティに 参加します。詳しくは4月号のニュースをご確認ください。 -
2022.4.15
4月号後半の記事をアップしました
-
2022.4.1
4月号の記事をアップしました
-
2022.3.15
3月号後半の記事をアップしました
-
2022.3.1
3月号の記事をアップしました
-
2022.2.15
2月号後半の記事をアップしました
-
2022.2.1
2月号の記事をアップしました
-
2022.1.17
1月号後半の記事をアップしました
-
2022.1.5
1月号の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JA3YUA」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2021.12.15
12月号後半の記事をアップしました
-
2021.12.1
12月号の記事をアップしました
-
2021.11.15
11月号後半の記事をアップしました
-
2021.11.01
2021年11月号の記事をアップしました
-
2021.10.15
10月号後半の記事をアップしました
-
2021.10.01
2021年10月号の記事をアップしました
-
2021.09.15
9月号後半の記事をアップしました
-
2021.09.01
2021年9月号の記事をアップしました
-
2021.08.16
8月号後半の記事をアップしました
-
2021.08.02
2021年8月号の記事をアップしました
-
2021.07.15
7月号後半の記事をアップしました
-
2021.07.01
2021年7月号の記事をアップしました
-
2021.06.15
6月号後半の記事をアップしました
-
2021.06.01
2021年6月号の記事をアップしました
-
2021.05.17
5月号後半の記事をアップしました
-
2021.05.06
2021年5月号の記事をアップしました
-
2021.04.15
4月号後半の記事をアップしました
-
2021.04.01
2021年4月号の記事をアップしました
連載記事 Masacoの「むせんのせかい」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.15
3月号後半の記事をアップしました
連載記事「今月のハム」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.01
2021年3月号の記事をアップしました
-
2021.02.15
2月号後半の記事をアップしました
-
2021.02.01
2021年2月号の記事をアップしました
-
2021.01.15
1月号後半の記事をアップしました
-
2021.01.05
2021年1月号の記事をアップしました
-
2020.12.15
12月号後半の記事をアップしました
-
2020.12.01
2020年12月号の記事をアップしました
-
2020.11.16
11月号後半の記事をアップしました
-
2020.11.02
2020年11月号の記事をアップしました
-
2020.10.15
10月号後半の記事をアップしました
-
2020.10.01
2020年10月号の記事をアップしました
-
2020.09.15
9月号後半の記事をアップしました
-
2020.09.01
2020年9月号の記事をアップしました
-
2020.08.17
8月号後半の記事をアップしました
-
2020.08.03
2020年8月号の記事をアップしました
-
2020.07.15
7月号後半の記事をアップしました
-
2020.07.01
2020年7月号の記事をアップしました
-
2020.06.15
6月号後半の記事をアップしました
-
2020.06.01
2020年6月号の記事をアップしました
-
2020.05.01
2020年5月号の記事をアップしました
-
2020.04.15
4月号後半の記事をアップしました
-
2020.04.01
2020年4月号の記事をアップしました
-
2020.03.16
3月号後半の記事をアップしました
-
2020.03.09
JARD、eラーニングでのアマチュア無線国家資格取得を呼び掛けるお知らせを、臨時休校で自宅待機中の小中高生に向けて発表。詳しくはこちら。
-
2020.03.02
2020年3月号の記事をアップしました
-
2020.02.17
2月号後半の記事をアップしました
-
2020.02.03
2020年2月号の記事をアップしました
-
2020.01.15
1月号後半の記事をアップしました
-
2020.01.06
2020年1月号の記事をアップしました
-
2019.12.16
12月号後半の記事をアップしました
-
2019.12.02
2019年12月号の記事をアップしました
-
2019.11.15
11月号後半の記事をアップしました
-
2019.11.01
2019年11月号の記事をアップしました
-
2019.10.15
10月号後半の記事をアップしました
-
2019.10.01
2019年10月号の記事をアップしました
-
2019.09.17
9月号後半の記事をアップしました
-
2019.09.02
2019年9月号の記事をアップしました
-
2019.08.16
8月号後半の記事をアップしました
-
2019.08.01
2019年8月号の記事をアップしました
-
2019.07.16
7月号後半の記事をアップしました
-
2019.07.01
2019年7月号の記事をアップしました
-
2019.06.17
6月号後半の記事をアップしました
-
2019.06.01
2019年6月号の記事をアップしました
-
2019.05.20
5月号後半の記事をアップしました
-
2019.05.07
2019年5月号の記事をアップしました
-
2019.04.15
4月号後半の記事をアップしました
-
2019.04.01
2019年4月号の記事をアップしました
-
2019.03.15
3月号後半の記事をアップしました
-
2019.03.01
2019年3月号の記事をアップしました
-
2019.02.15
2月号後半の記事をアップしました
-
2019.02.01
2019年2月号の記事をアップしました
-
2019.01.18
1月号後半の記事をアップしました
-
2019.01.07
2019年1月号の記事をアップしました
-
2018.12.17
12月号後半の記事をアップしました
-
2018.12.01
2018年12月号の記事をアップしました
-
2018.11.15
11月号後半の記事をアップしました
-
2018.11.01
2018年11月号の記事をアップしました
-
2018.10.15
10月号後半の記事をアップしました
-
2018.10.01
2018年10月号の記事をアップしました
-
2018.09.15
9月号後半の記事をアップしました
-
2018.09.01
2018年9月号の記事をアップしました
-
2018.08.17
8月号後半の記事をアップしました
-
2018.08.01
2018年8月号の記事をアップしました
-
2018.07.17
7月号後半の記事をアップしました
-
2018.07.02
2018年7月号の記事をアップしました
-
2018.06.15
6月号後半の記事をアップしました
-
2018.06.01
2018年6月号の記事をアップしました
-
2018.05.15
5月号後半の記事をアップしました
-
2018.05.01
2018年5月号の記事をアップしました
-
2018.04.16
4月号後半の記事をアップしました
-
2018.04.02
2018年4月号の記事をアップしました
-
2018.03.15
3月号後半の記事をアップしました
-
2018.03.01
2018年3月号の記事をアップしました
-
2018.02.15
2月号後半の記事をアップしました
-
2018.02.01
2018年2月号の記事をアップしました
-
2018.01.15
1月号後半の記事をアップしました
-
2018.01.05
2018年1月号の記事をアップしました
-
2017.12.15
12月号後半の記事をアップしました
-
2017.12.1
12月号をアップしました
-
2017.11.15
11月号後半の記事をアップしました
-
2017.11.1
11月号をアップしました
-
2017.10.16
10月号後半の記事をアップしました
-
2017.10.2
10月号をアップしました
-
2017.9.15
What a healthy time! ~健康を応援する特別なお料理~/第3回 食物繊維たっぷり! 海藻の和風リゾット、FB Monthly Fashion/第9回 秋っぽい柄&色コーデ、子供の無線教室/第9回 「アンテナの形や大きさに注目!!」を掲載しました
-
2017.9.4
<速報>ハムフェア2017を掲載しました
-
2017.9.1
9月号をアップしました
-
2017.8.17
What a healthy time! ~健康を応援する特別なお料理~/第2回 和風のポトフ 納豆ソース添え、FB Monthly Fashion/第8回 夏のお出かけコーデ、子供の無線教室/第8回 「無線機にはどんなものがあるの?」を掲載しました
-
2017.8.1
8月号をアップしました
-
2017.7.18
What a healthy time! ~健康を応援する特別なお料理~/第1回 メロンの冷製スープ ナッツのアイスクリームのせ、FB Monthly Fashion/第7回 コットンTシャツコーデとボーイズコーデ、子供の無線教室/第7回 「電波はどうやって海外や宇宙に届くの?」を掲載しました
-
2017.7.1
7月号をアップしました
-
2017.6.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第9回 FB Girlsの野望 with ムースと甘エビのタルタル、FB Monthly Fashion/第6回 雨の日コーデと親子コーデ、子供の無線教室/第6回 「電波はいろいろなところで大活躍!!」を掲載しました
-
2017.6.1
6月号をアップしました
-
2017.5.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第8回 番外編 春うらら♪豪華弁当でお花見、FB Monthly Fashion/第5回 ブラウス&シャツを使ったコーディネート、子供の無線教室/第5回 「周波数によって変わる、電波の特徴」を掲載しました
-
2017.5.1
5月号をアップしました
-
2017.4.17
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第7回 ARDFの思い出 with 2種類のソースのカルボナーラ、FB Monthly Fashion/第4回 Gジャンを使ったコーディネート、子供の無線教室/第4回 「電波の性質を覚えよう」を掲載しました
-
2017.4.1
4月号をアップしました
-
2017.3.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第6回 初めてのQSOの思い出 with グリーンのアクアパッツァ、FB Monthly Fashion/第3回 ピンクを使ったコーディネート、子供の無線教室/第3回 「電波はどうやって伝わるの?」を掲載しました
-
2017.3.1
3月号をアップしました
-
2017.2.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第5回 FB Girlsの試験の思い出 withウマ辛和風スープ、FB Monthly Fashion/第2回 デニムと明るめニットのコーディネートを掲載しました
-
2017.2.1
2月号をアップしました
-
2017.1.16
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第4回 YLハムを増やす秘策とは?! withおなかにやさしいお料理、【新連載】FB Monthly Fashion/第1回 アウター別おすすめコーディネート(ライダース・ノーカラー・ダッフル)を掲載しました
-
2017.1.5
1月号をアップしました
-
2016.12.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第3回 YLハムの行く年来る年 with ブイヤベースの洋風お鍋を掲載しました
-
2016.12.1
12月号をアップしました
-
2016.11.15
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(後編)!、What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第2回 YLハムの悩み解決!with サケのフレンチトーストを掲載しました
-
2016.11.1
11月号をアップしました
-
2016.10.17
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(前編)!、【新連載】What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第1回 FB GirlsのプライベートQSO with 土瓶蒸しのリゾットを掲載しました
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)
次号は 12月 1日(木) に公開予定