第12話では非線形歪みが伝送信号をどのように劣化させるのかについて解説しました。基本的に非線形歪みは増幅器やミキサなど電子回路で発生し、伝送信号の振幅が大きいほど強く影響を受ける劣化です。一方で信号の振幅が小さくなると熱雑音のレベルが相対的に上昇するため、やはり伝送信号は劣化することになります。このため電子回路の中においては信号振幅の設定は慎重に行う必要があります。第13話では非線形歪みの影響を(強く)受けない範囲で、できるだけ大きな振幅を取り扱うために必要な知識について解説します。

1. (改めて)交流の電圧と電力

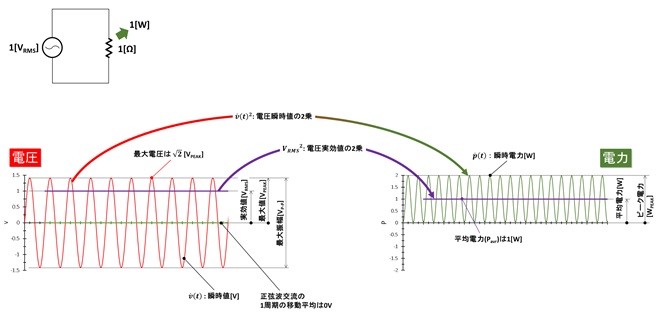
交流電圧の表記方法と電力の関係は電気工学の授業の最初に登場する話なので、「そんなの知ってるよ」とお叱りを受けそうですが、レベルダイヤグラム上で変調信号のレベルの議論をしていると、怪しくなることが多々あるので、ここで一度復習です。図1は単一周波数で振幅が一定の交流信号(家庭に引き込まれているAC100V交流も含む)の電圧の表現方法、ならびに電力との関係を示したものです。

図1 交流電圧とその表現方法、ならびに電力の関係

交流電圧(正弦波交流)の最大の特徴は時間とともに大きさと極性が変化するところにあります。このため交流電圧の大きさには以下に示す複数の表現方法が存在します。

• ①瞬時値[V]: 変化する電圧のある瞬間の値を示します。この値は振幅と位相の情報を持つベクトル量で時間の関数(周期関数)です。
• ②最大振幅[V_P-P]: オシロスコープで波形観測した時に振幅の大きさを表現するのに使用する値で、交流振幅の＋のピークから－のピークまでの大きさを示します。
• ③最大値[V_PEAK]: 正弦波の片方の山の最大値を示します。
• ④実効値[V_RMS]: 二乗平均の平方根･･･ すなわち等平均電力となる直流電圧換算値を示します。

また交流電力を表現する方法としては

• ⑤瞬時電力[W＋jVar]: 交流電圧が印加されている負荷が消費する、ある瞬間の電力で時間の関数です。有効電力と無効電力から構成されるベクトル量です。
• ⑥ピーク電力(最大電力)[W_PEAK]: 周期変動する電力の最大値を示します。
• ⑦平均電力[W]: 負荷で消費される電力の平均値を示します。

交流電圧には「平均電圧」の定義^※1も存在しますが、ここでは敢えて省略しました。何故かというと交流電圧(電流)は正負が対称になる振動なので、1サイクルの平均値は必ず0[V]になるからです。一方で電力には「平均電力」が存在します。ここで負荷抵抗R=1[Ω]とおくと、電圧と電力の関係は

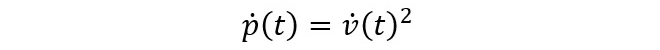
(式1-1)

従って交流電力は時間とともに変動する値ですが極性は反転しません(マイナスの電力を消費するということは、負荷からエネルギーが湧き出している状態を示します)。

正弦波交流の場合、1サイクルの平均電力P_AVERAGE とピーク電力P_PEAK は三角関数のべき乗公式から、(式1-2)に示す関係となります。

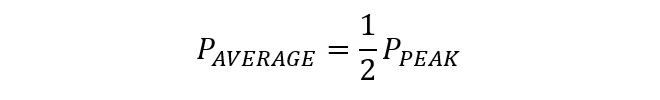
(式1-2)

従って、図2に示すように電圧最大値が1[V_PEAK]一定の正弦波電圧が印加される1[Ω]の負荷抵抗が消費する電力は、ピーク値が1[W]、平均値が0.5[W]となります。直流回路であれば1[Ω]の負荷抵抗に1[V]の電圧を印加したときの負荷抵抗の消費電力は

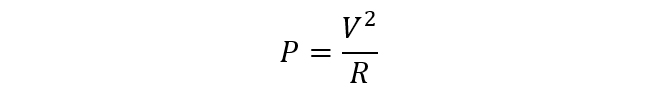
(式1-3)

なので1[W]と算出されるのですが、交流電圧を最大値で表記すると、実際に電気エネルギーの行った仕事は平均電力の関数となるため、この関係式に補正が必要になって面倒です。そこで平均電力との関係が(式1-3)になる電圧値として(式1-4)に示す実効値が定義されています。

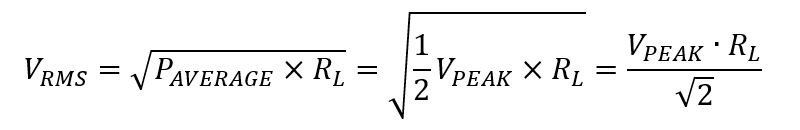
RL=1[Ω]のとき、

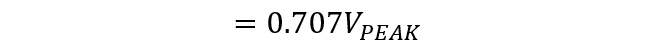
(式1-4)

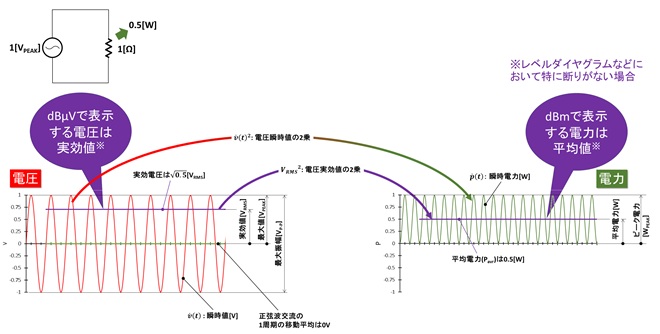
図2 ピーク値を基準にした場合の交流電圧とその表現方法、ならびに電力の関係

筆者は個人的に図1の表現よりも図2の表現で電圧と電力の関係を説明する方が理解しやすいと思うのですが、世間一般には図1で電圧と電力の説明をするのが一般的ではないかと思います。

実効値を定義することにより、平均電力の計算は直流と同様、実効値電圧×実効値電流、もしくは実効値電圧^２÷負荷抵抗とすることができるので、消費電力に課金する商用交流の電圧表記は特に断りがない場合は実効値を表しています。

※1 電気工学において、正弦波交流の平均電圧・平均電流は、絶対値の平均値と定義されています。

2. 交流電圧表記法とdBm・dBμV

信号の世界では、交流電力の表記にデシベル(dBm)を用います。dBmは瞬時電力、ピーク電力、平均電力の何れにも適用するので読む側で注意が必要です。レベルダイヤグラム上で「信号レベル」として使用される「dBm」は平均電力を示します。従って第4話の表1で解説したようなdBmから換算したdBμVは平均電力と紐付けされる必要があるので実効値ということになります(V_log[dBμV]=20logV[μV]の定義なので、そもそも電力換算値だと考えるべきです)。実効値以外の電圧にもdBμVが適用されるケースがありますが、この場合は電力のdBに換算できない(換算しても意味が無い)ケースが存在しますので注意が必要です。

3. 変調信号の電力とPAPR

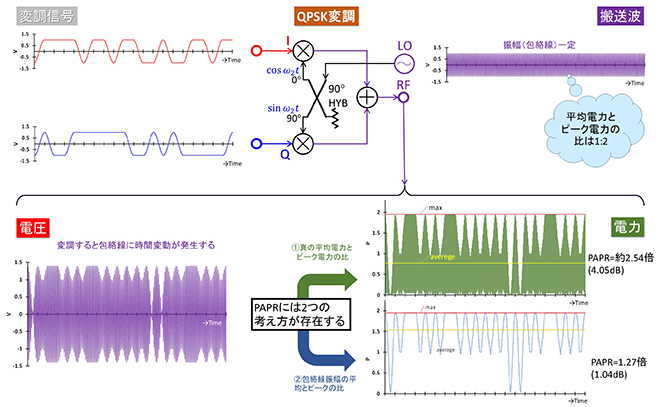
ここまでは振幅一定の交流に関する電圧と電力の関係を解説しましたが、実際に通信に使用する信号は交流(搬送波)の振幅や位相(もしくは周波数)に伝送したい情報を載せます。これを変調と呼びます。伝送情報で変調された交流はその振幅が変調情報に対応して変化します。その様子をQPSKを例にとってExcelで計算した結果が図3です。

図3 QPSK変調波のピーク電力と平均電力

図1、図2と同様、紫のグラフは電圧を示し、緑のグラフは電力を示します。QPSK変調は2ビットのビット列(インパルス列)を、MSB、LSBそれぞれコサインロールオフフィルタで帯域制限された振幅±1のベースバンド信号(シリアル伝送信号: 赤と青のグラフ)に変換し、直交搬送波のi軸、q軸それぞれに乗算するので、変調された信号の振幅にはベースバンド信号の波形に対応した振幅変化が発生します。従ってQPSK変調波の平均電力とピーク電力の比は搬送波(振幅一定の正弦波交流)と比べて大きくなります。

信号の平均電力とピーク電力の比を“ピーク対平均電力比”: PAPR(Peak/Average Power Ratio)と呼びます。文字通り変調信号の平均電力とピーク電力の電力比をdBで示したパラメータです。なお世間で使われているPAPRには2種類の定義があります。

①信号の平均電力とピーク電力の比
②信号の包絡線の平均電力とピーク電力の比

“①”の定義は読んで文字のごとくなのであまり違和感がないと思います。(式1-2)に示したとおり、無変調の正弦波の平均電力の値はピーク値の0.5倍なのでPAPRは3dB、QPSK,QAM等の変調波や周波数の異なるサイン波の集合体はこれより大きな値になります。“②”は変調された信号そのものではなく、変調された信号の包絡線の平均電力とピーク電力の比を示すもので、ピーク電力は“①”と同じ値をとりますが、平均電力は無変調交流の最大値と等しくなります。 これは無変調の正弦波や定包絡線変調(FMやFSK)のPAPRを0dBとおきたい時に用いる定義で、世間一般にはこちらが主流のように見えます。あまり区別せずに使用されているようですが、両者の間で3dBの隔たりが生じるので注意が必要です。

次ページは「PAPRとバックオフ」