第11話では「非線形歪み(ひずみ)」とは入力信号がn乗された成分であること、そして、その発生理由は、

①トランジスタ等を構成する半導体のpn接合の電圧対電流特性が指数関数であること
②入力信号の振幅が大きすぎると、電源電圧の制約で出力振幅のクリップが発生することに

の二つが存在する事を解説しました。第12話では引き続き、入力信号のn乗成分が何故伝送信号を劣化させるのかについて解説します。

1. 2トーン信号をn乗したときのスペクトル(お詫び)

第11話の図5で2つのスペクトル(𝑓₁+𝑓₂信号)を2乗、3乗したときに生成されるスペクトルを示しましたが、うっかり周波数の離れた二つのスペクトルの事例を掲載しました。これは周波数変換回路(ミキサー回路)の動作を説明するときの図なので、帯域幅のある信号を2乗、3乗したときのスペクトルをイメージするには難しかったのではないかと思います。改めて2トーン信号(2つのスペクトルから構成される信号)、すなわち周波数の近い2つのスペクトル(𝑓₁+𝑓₂信号)を2乗、3乗したときに生成されるスペクトルを図1に示します。

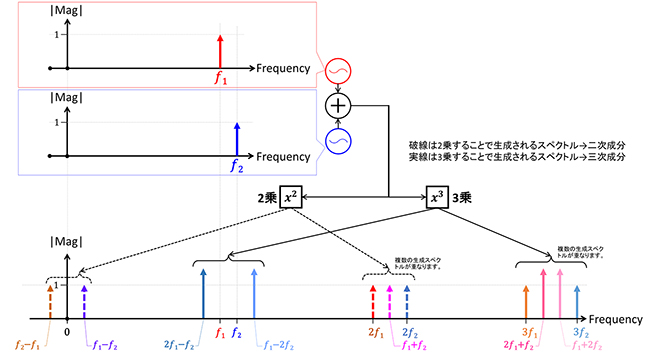
図1 2トーン信号(𝑓₁+𝑓₂信号)を2乗、3乗したときに生成されるスペクトル

これは変調信号をイメージしたもので、2つのスペクトル𝑓₁、𝑓₂の中間が搬送波周波数(いわゆるチャネル周波数)と考えてください。図から判るように、2つのスペクトルを2乗した結果発生するスペクトル(破線)は0倍周波数(DC)と2倍周波数、3乗した結果発生するスペクトル(実線)は1倍周波数と3倍周波数付近となります。2乗した結果発生するスペクトル成分を二次成分(または二次高調波)、3乗した結果のそれを三次成分(または三次高調波)と呼びます(数学でいう多項式の次数と同じです)。一般的な表現で言い直すと、

• ・サイン波をn乗(n=奇数)すると、そのスペクトルは入力周波数の1次～n次(1倍～n倍)までの奇数次のスペクトルに置き換えらる。
• ・サイン波をm乗(m=偶数)すると、そのスペクトルは入力周波数の0次～m次(0倍～m倍)までの偶数次のスペクトルに置き換えられる。

という事になります。

2. 変調波(帯域幅のある信号)をn乗したときのスペクトル

実際に伝送情報が載った変調信号は𝑓₁と𝑓₂の間にも無数のスペクトルが存在する事になるので、図1は図2のように変化します。

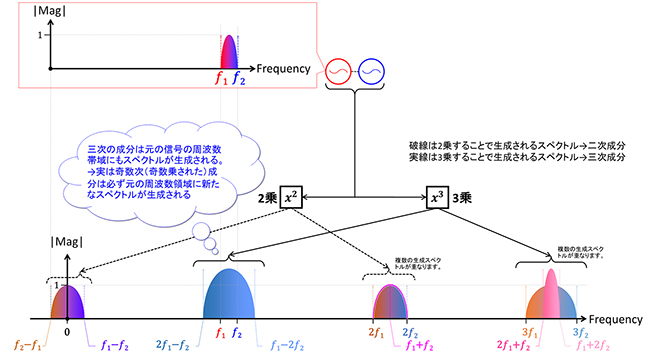
図2 帯域幅𝑓₂－𝑓₁の変調信号を2乗、3乗したときに生成されるスペクトル

図2では図1との対応関係を判りやすくするため、2つのスペクトル𝑓₁、𝑓₂とその2乗、3乗結果も細い線で並記しています。変調波を2乗した結果発生するスペクトルは、その帯域幅が2倍になり、0倍周波数(DC)と2倍周波数に、3乗した結果発生するスペクトルは、その帯域幅が3倍になり、1倍周波数と3倍周波数にそれぞれ発生します。先と同様、一般的な表現で言い直すと、

• ・帯域幅のある信号をn乗(n=奇数)すると、そのスペクトルは帯域幅がn倍になり、入力周波数の1次～n次(1倍～n倍)までの奇数次のスペクトルに置き換えられる。
• ・帯域幅のある信号をm乗(m=偶数)すると、そのスペクトルは帯域幅がm倍になり、入力周波数の0次～m次(0倍～m倍)までの偶数次のスペクトルに置き換えられる。

という事になります。

ここまで解説すると察しの良いかたは「三次(奇数次)の成分は元の信号に干渉する」と気づかれた事と思います。ここまではサイン波を意図的に2乗、3乗した結果を見てきました。次節では、引き続き実際の増幅器で非線形歪みが発生した時、これらn乗、m乗成分がどのように信号に重畳するのかを見てみることにします。

3. 増幅器が歪んだときのスペクトル

サイン波(変調波も)をn乗、m乗すると、元の信号スペクトルはなくなってしまう。というのが図1、図2が示すところですが、実際の増幅器では指数関数特性で増幅されるのであって、入力信号の全てをn乗、m乗する訳ではありません。指数関数特性の増幅器で増幅された出力信号は、第11話の(式2-3)が示すように、自信号に高次歪みの成分が足し合わされたものとなります^※1。この様子を図3に示します。

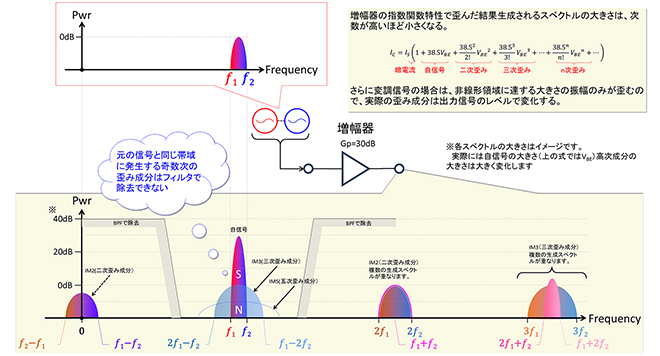
図3 帯域幅𝑓₂－𝑓₁の変調信号を大振幅動作の増幅器で増幅した場合の出力イメージ

増幅器の指数関数特性に起因して生成される高次のスペクトルは、図の右上の数式に朱書きしたとおり、“次数の階乗”分の1(例えば三次成分は)の係数がかかるので、次数が高くなるほど急激に小さい振幅になります。回路設計者が通常、三次歪み以上の高次の歪みを気にしないのはこのためです^※2。自信号と高次成分が足し合わされるため、前節の最後で触れたとおり、自信号には奇数次の1倍波成分が重なります。高次成分の0倍波と2倍波以上の成分はフィルタで分離することが可能なので、きちんと設計すれば伝送信号の劣化に寄与することは回避できますが、奇数次歪みの1倍波、中でも最もレベルが大きい三次歪みの1倍波成分は、重畳すると自信号と分離することが出来ないため、伝送信号を劣化させる事になります。劣化の程度は自信号に重畳される1倍波成分の電力を“等価雑音(N)”と見立てて計算することが可能です。歪みのスペクトルは自信号のスペクトルを次数倍に引き延ばしたような分布になるので、そのうちの自信号帯域分が劣化に寄与する等価雑音になりますが、大雑把な配分計算では隣接チャネル漏洩電力として見えている大きさ(電力密度)と同じ大きさ(電力密度)の電力が自帯域内に存在すると仮定して計算したり、見えている値＋1.5～3dB程度の電力密度と見なして計算する場合もあります。

• ※1: 第11話の(式2-2)～(式2-3)に下記の通り誤記がありました。お詫びして訂正いたします。図3に記載の数式は訂正後のものとなっています。

 図3に示したように、トランジスタのベース・エミッタ間電圧V_BEとコレクタ電流I_Cの間
 には以下の関係があります

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(式2-1)
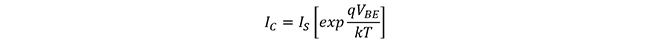
 但し、I_Sは逆方向飽和電流(デバイス依存の定数)、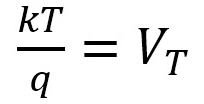 (熱電圧)=26mv @300K なので、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(式2-2)
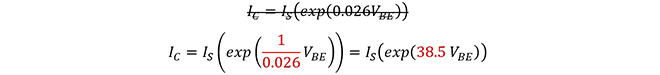
 指数関数は級数に展開することが可能で、マクローリン展開すると

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(式2-3)
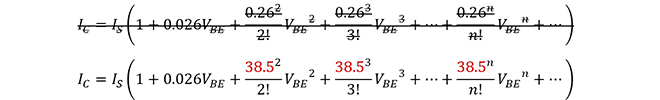
 となります。

• ※2: 高ダイナミックレンジが要求されるシステムでは五次、七次あたりまでケアが必要になる場合があります。

次ページは「周波数変換回路が歪んだときのスペクトル」